Calculer la Probabilité d’une Issue
Théorie
En Cinquième, les calculs de probabilité s’effectuent dans des situations d’équiprobabilité. Calculer la probabilité d’une issue consiste à déterminer les chances d’obtenir cette issue à la fin de l’expérience.
Exemple
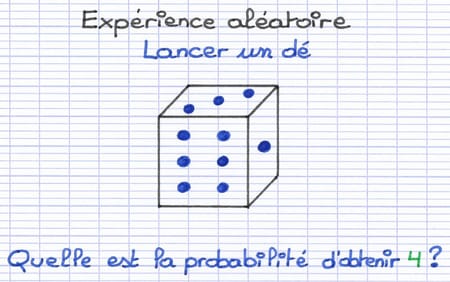
On lance un dé équilibré à 6 faces numérotées de 1 à 6, puis on lit le numéro de la face supérieure. Comment calculer la probabilité d’obtenir l’issue "4" ?
1. Compter le Total d’Issues
Une expérience aléatoire possède plusieurs issues. Pour calculer une probabilité, on commence par compter le nombre total d’issues différentes.
Le nombre total d’issues de cette expérience aléatoire est 6.
2. Écrire la Probabilité
En situation d’équiprobabilité, la probabilité d’une issue est une fraction dont :
- Le numérateur est le chiffre 1.
- Le dénominateur est le nombre total d’issues.
Le numérateur de la fraction est donc toujours inférieur ou égal au dénominateur.
La probabilité d’obtenir l’issue "4" est la fraction 1/6. On a 1 chance sur 6 d’obtenir "4" quand on lance le dé.
La probabilité d’une issue peut également s’écrire en pourcentage ou nombre décimal. Les différentes formes d’écriture d’une probabilité sont abordées en Quatrième.
Équiprobabilité
Dans une situation d’équiprobabilité, chaque issue a une probabilité identique de se réaliser. En calculant la probabilité d’obtenir une issue, on obtient du même coup la probabilité d’obtenir chacune des autres issues.
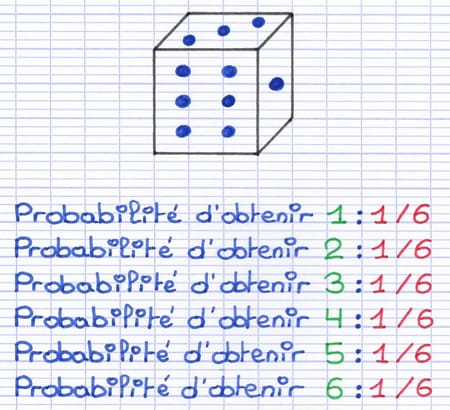
Lancer un dé équilibré est une situation d’équiprobabilité. La probabilité de chaque issue est identique : 1/6. On a 1 chance sur 6 d’obtenir chaque numéro.
Exercices
Question 1
On tourne une roue partagée équitablement en quatre zones de couleur : rouge, vert, rose et bleu. On observe ensuite la couleur obtenue. Quelle est la probabilité d’obtenir la couleur rouge ?
Question 2
Laquelle de ces propositions est fausse ?
Question 3
On lance une pièce de monnaie truquée, puis on observe si la pièce est tombée sur pile ou face. Quelle est la probabilité d’obtenir face ?