Construire l’Image d’un Point par Translation
Théorie
Une translation est une transformation géométrique correspondant à un déplacement rectiligne. La construction de l’image d’un point par translation s’effectue à partir d’un vecteur.
Exemple
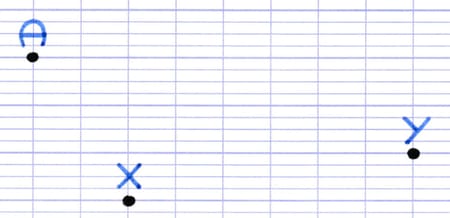
Comment construire l’image du point A par la translation qui transforme X en Y ?
Tracer le Vecteur de la Translation
Un vecteur est une flèche qui relie un point à son image par translation. Dans cet exemple, la translation transforme X en Y, ce qui signifie que :
- Y est l’image du point X par la translation.
- Le vecteur de la translation est la flèche qui relie X à Y.
La 1re étape est de tracer la flèche entre ces deux points pour faire apparaître le vecteur de la translation.
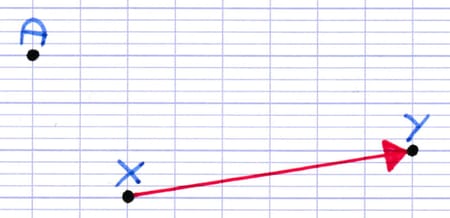
La flèche rouge est le vecteur de la translation qui transforme X en Y.
Le vecteur indique les 3 caractéristiques de la translation : direction, sens et longueur.
Construire un Vecteur Parallèle
On identifie ensuite le point dont on souhaite construire l’image (le point A). À partir de ce point, on trace un 2e vecteur identique au vecteur de la translation. Ce 2e vecteur doit être parallèle, de même sens et de même longueur que le vecteur de la translation.
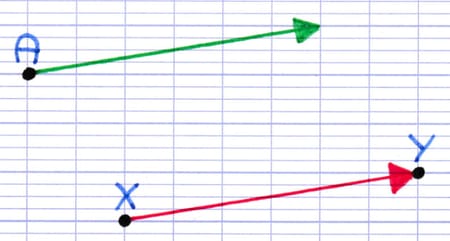
La construction du vecteur parallèle démarre du point A. Le vecteur vert possède les mêmes caractéristiques (direction, sens et longueur) que le vecteur rouge.
Les deux vecteurs représentent la même translation, sauf que :
- Le vecteur rouge permet de trouver l’image du point X.
- Le vecteur vert permet de trouver l’image du point A.
Trouver l’Image du Point
Chaque vecteur de translation indique la position de l’image d’un point :
- Le point de départ du vecteur est le point d’origine.
- Le point d’arrivée du vecteur est l’image du point d’origine.
L’image du point A se situe donc à l’extrémité du vecteur qui démarre du point A.
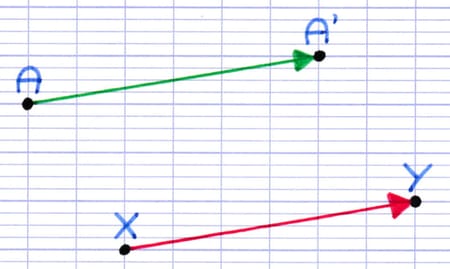
A’ est l’image du point A par la translation qui transforme X en Y.
Pour nommer l’image d’un point, on utilise généralement la même lettre. On y ajoute cependant une apostrophe afin de la distinguer du point d’origine : A’ est l’image de A.