Découvrir les Caractéristiques du Parallélogramme
Théorie
Un parallélogramme est un quadrilatère qui possède de nombreuses particularités. La principale caractéristique du parallélogramme est de posséder des côtés opposés de même longueur et parallèles.
Quelles sont les propriétés caractéristiques du parallélogramme ?
Côtés Opposés
Le parallélogramme est un quadrilatère, il possède donc 4 côtés. Ses côtés opposés (face à face) ont la particularité d’être parallèles et de même longueur.
![Parallélogramme ABCD avec côtés opposés parallèles et de longueur identique : [AB] et [DC], ainsi que [AD] et [BC].](/img/fiche/210/cotes-opposes-parallelogramme-paralleles-longueur-identique.jpg "Côtés opposés d’un parallélogramme parallèles et de longueur identique")
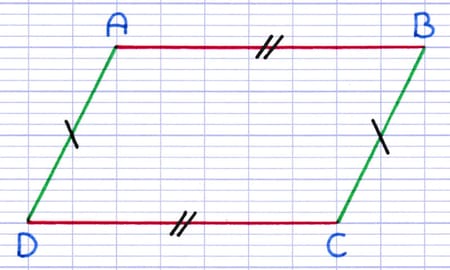
Les 2 côtés opposés [AB] et [DC] sont parallèles et de longueur identique.
Les 2 côtés opposés [AD] et [BC] sont parallèles et de longueur identique.
Pour démontrer qu’un quadrilatère est un parallélogramme, on peut utiliser la propriété ci-dessous.
Propriété : "Si les côtés opposés d’un quadrilatère sont parallèles et de même longueur, alors c’est un parallélogramme".
Angles Opposés
Le parallélogramme est un quadrilatère, il possède donc 4 angles dont la somme est égale à 360°. Ses angles opposés (face à face) ont la particularité d’être de la même mesure.
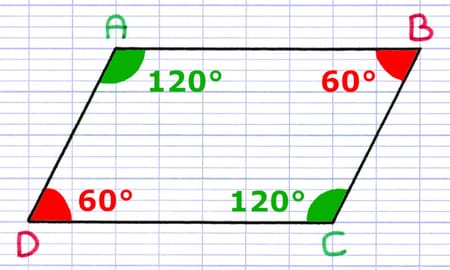
Les 2 angles opposés DAB et BCD mesurent chacun 120°.
Les 2 angles opposés ABC et CDA mesurent chacun 60°.
La somme des angles du parallélogramme est égale à 360° (60° + 120° + 60° + 120°).
Pour démontrer qu’un quadrilatère est un parallélogramme, on peut utiliser la propriété ci-dessous.
Propriété : "Si les angles opposés d’un quadrilatère sont de même mesure, alors c’est un parallélogramme".
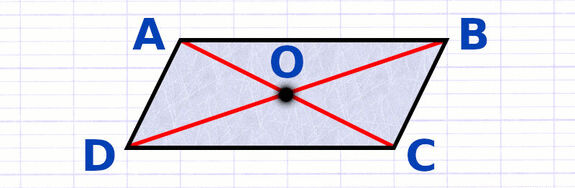
Diagonales
Le parallélogramme est un quadrilatère, il possède donc 2 diagonales qui relient les sommets opposés. Ses diagonales ont la particularité de se couper en leur milieu.
![Parallélogramme ABCD avec ses deux diagonales [AC] et [BD] se coupant en leur milieu, le point O.](/img/fiche/210/diagonales-parallelogramme-coupent-milieu.jpg "Diagonales d’un parallélogramme se coupant en leur milieu")
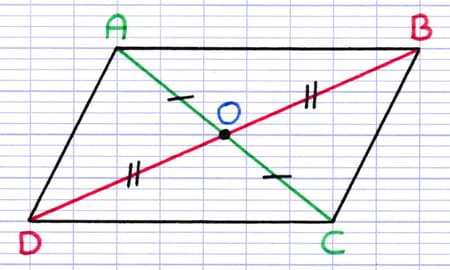
[AC] et [BD] sont les 2 diagonales du parallélogramme.
Leur point d’intersection (le point O) est le milieu des 2 diagonales.
AO = OC et BO = OD
Pour démontrer qu’un quadrilatère est un parallélogramme, on peut utiliser la propriété ci-dessous.
Propriété : "Si les diagonales d’un quadrilatère se coupent en leur milieu, alors c’est un parallélogramme".
Centre de Symétrie
Le parallélogramme est le seul quadrilatère à posséder un centre de symétrie. Le losange, le rectangle et le carré ont également un centre de symétrie, ces trois figures sont des parallélogrammes particuliers. Le centre de symétrie du parallélogramme est le point d’intersection de ses diagonales.
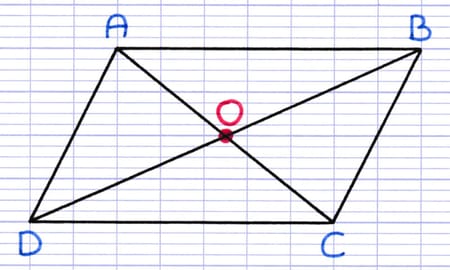
Le point O est le centre de symétrie du parallélogramme.
Pour démontrer qu’un quadrilatère est un parallélogramme, on peut utiliser la propriété ci-dessous.
Propriété : "Si un quadrilatère possède un centre de symétrie, alors c’est un parallélogramme".
Quiz
Question 1
Quelle est la mesure de l’angle ABC de ce parallélogramme ?
Question 2
Laquelle de ces propriétés est fausse ?
Question 3
Sachant que [AC] et [BD] sont les diagonales du parallélogramme et que AO = 4 cm, quelle est la longueur de la diagonale [BD] ?