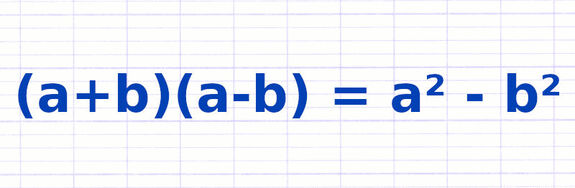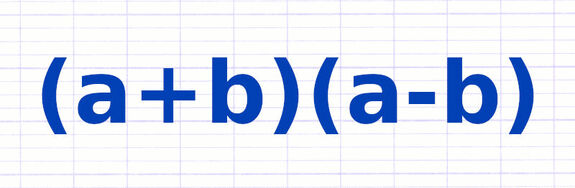Démontrer l’Identité Remarquable (a+b)(a-b) = a²-b²

🎯

Questions validées : 0 / 3

Théorie

Une identité remarquable est une égalité entre deux expressions littérales. La démonstration algébrique de l’identité remarquable (a+b)(a-b) = a²-b² s’effectue en deux étapes.

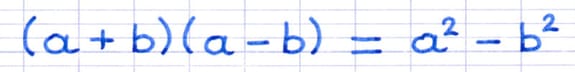
Démontrer l’identité remarquable de la différence de 2 carrés — Comment démontrer l’identité remarquable **(a+b)(a-b) = a²-b²** ?

Développer l’Expression

L’expression gauche de l’identité remarquable est un produit de deux parenthèses : (a+b) et (a-b). La 1^re étape est de développer cette expression en effectuant la double distributivité. Le résultat obtenu est une expression développée sans aucune parenthèse.

Développement de l’identité remarquable par la double distributivité — La **double distributivité** permet de développer l’expression gauche de l’identité remarquable.

Fiche de Synthèse

Distributivité Double - Développer une Expression Littérale

Réduire l’Expression

L’expression développée possède deux termes de même famille : -ab et +ab. Il est donc possible de réduire cette expression, car ces deux termes s’annulent.

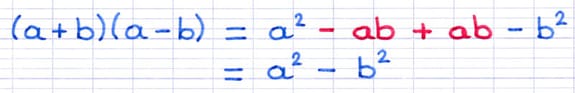
Réduction de l’identité remarquable — La **réduction** permet d’obtenir l’expression droite de l’identité remarquable.

Fiche de Synthèse

Réduire une Expression Littérale

Le résultat obtenu est identique à l’expression droite de l’identité remarquable. (a+b)(a-b) est donc égal à a² - b², la démonstration est terminée !