Démontrer qu’un Triangle est Rectangle avec Pythagore
Théorie
Réciproque du théorème de Pythagore : Un triangle est rectangle si le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés.
En connaissant la longueur des 3 côtés d’un triangle, on peut utiliser la réciproque de Pythagore pour vérifier qu’un triangle est rectangle.
Démonstration
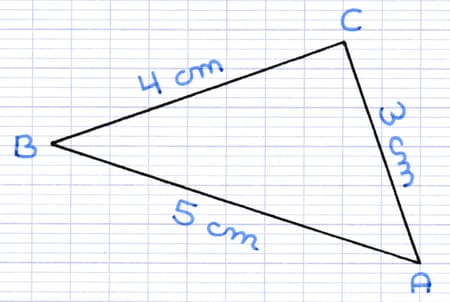
Comment démontrer que ce triangle est rectangle avec la réciproque du théorème de Pythagore ?
Calculer le Carré du Plus Grand Côté
Tous les triangles rectangles possèdent un côté plus grand que les autres (hypoténuse). La 1re étape est d’identifier le plus grand côté du triangle et de calculer le carré de sa longueur. Si le triangle ne possède pas de plus grand côté, alors il n’est pas rectangle.
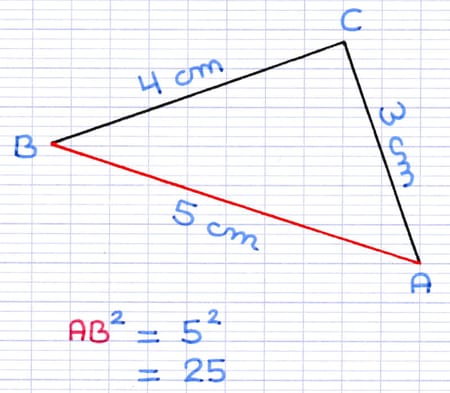
[AB] est le plus grand côté du triangle.
Le carré de la longueur de [AB] est 25.
Calculer la Somme des Carrés des Autres Côtés
L’étape suivante est d’additionner les carrés des longueurs des deux autres côtés. Les calculs s’effectuent en appliquant l’ordre de priorité des opérations (PEMDAS). Le carré des deux côtés est d’abord calculé, puis on additionne les résultats obtenus.
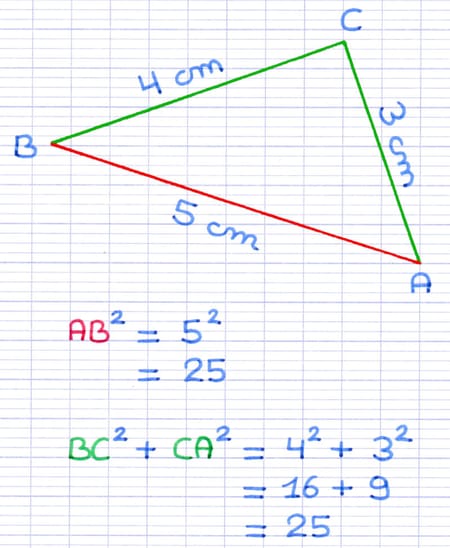
[BC] et [CA] sont les deux autres côtés du triangle. La somme des carrés de leur longueur est 25.
Comparer les 2 Résultats
Un triangle est rectangle si le carré du plus grand côté est égal à la somme des carrés des deux autres côtés. La dernière étape est de comparer les résultats obtenus à l’étape 1 et 2 :
- Si les résultats sont identiques, le triangle est rectangle.
- Si les résultats sont différents, le triangle n’est pas rectangle.
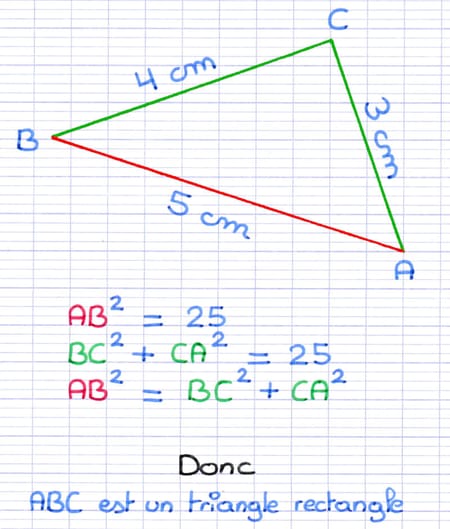
Le carré du plus grand côté (25) est égal à la somme des carrés des 2 autres côtés (25).
Cette comparaison démontre que le triangle est rectangle.
Conclusion : D’après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en C.
L’hypoténuse du triangle rectangle est [AB] (le plus grand côté).