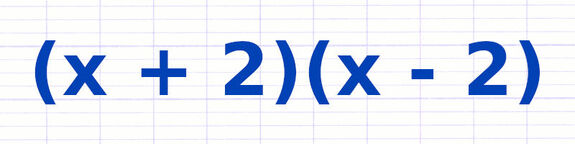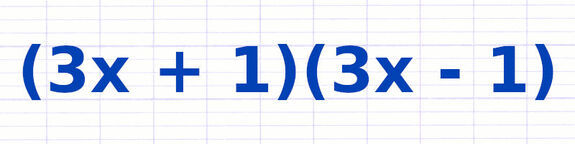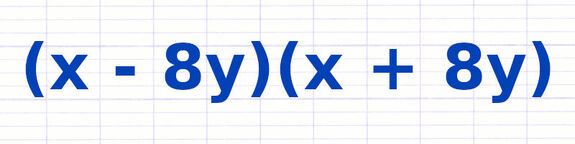Développer l’Identité Remarquable (a+b)(a-b)
Théorie
L’expression littérale « (a + b)(a - b) » est un produit de deux parenthèses. Le développement de cette expression peut s’effectuer à l’aide de la double distributivité. Il est cependant plus rapide et efficace d’appliquer la formule de l’identité remarquable.
Formule : « (a + b)(a - b) = a² - b² ».
Exemple
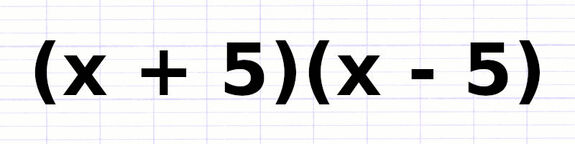
Comment développer l’identité remarquable (x + 5)(x - 5) ?
1. Reconnaître l’Identité Remarquable
La première étape est de s’assurer que l’expression littérale correspond bien à l’identité remarquable « (a + b)(a - b) ». Pour cela, on vérifie qu’il s’agit d’un produit de 2 parenthèses contenant chacune 2 termes dont :
- Les premiers termes de chaque parenthèse sont identiques.
- Les deuxièmes termes de chaque parenthèse sont opposés.
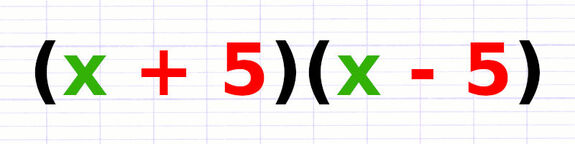
Les premiers termes sont identiques : x.
Les deuxièmes termes sont opposés : + 5 et - 5.
Au sein de l’identité remarquable « (a + b)(a - b) » :
- La première parenthèse est une somme.
- La deuxième parenthèse est une différence.
2. Identifier « a » et « b »
La deuxième étape est d’identifier les valeurs de « a » et « b » au sein de l’identité remarquable. Pour cela, on se réfère à la première parenthèse contenant une somme :
- Le premier terme correspond à la valeur de « a ».
- Le deuxième terme correspond à la valeur de « b ».
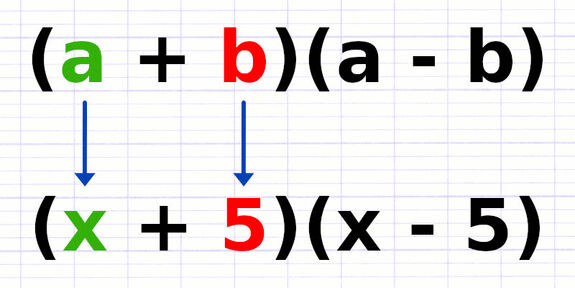
Au sein de l’identité remarquable :
La valeur de « a » est « x ».
La valeur de « b » est « 5 ».
3. Appliquer la Formule
Formule : « (a + b)(a - b) = a² - b² ».
D’après la formule de l’identité remarquable, le produit des deux parenthèses est égal à la différence des carrés des deux termes « a » et « b ».
Le résultat du développement s’obtient donc en élevant au carré chacun de ces deux termes. On n’oublie pas de noter le signe de la différence entre les deux carrés.
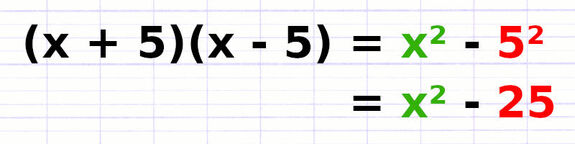
Si « (a + b)(a - b) = a² - b² ».
Alors « (x + 5)(x - 5) = x² - 5² ».
En élevant au carré, on obtient le résultat final « x² - 25 ».
Cas Particuliers
Parenthèses Inversées
L’ordre des parenthèses est parfois inversé : la première parenthèse est une différence, tandis que la deuxième est une somme.
Dans ce cas la formule à appliquer reste identique, sauf qu’on identifie « a » et « b » à partir de la deuxième parenthèse contenant la somme. Le résultat du développement de l’identité remarquable reste « a² - b² ».
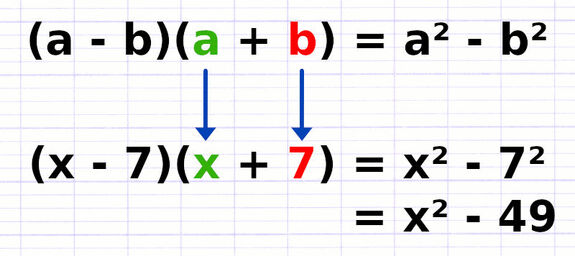
« (a - b)(a + b) » se développe de la même façon que « (a + b)(a - b) ».
Les multiplications sont commutatives, cela signifie que l’ordre des facteurs ne change pas le résultat :
- « 5 × 7 » est identique à « 7 × 5 ».
- « (a + b)(a - b) » est identique à « (a - b)(a + b) ».
Coefficients
Il est possible que les termes « a » et/ou « b » soient munis de coefficients. Dans ce cas, on prend en compte ces coefficients lorsqu’on élève les termes au carré.
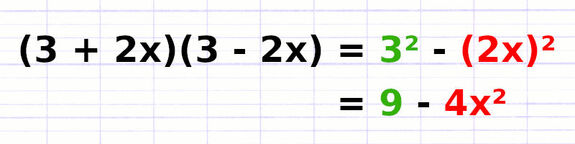
Si « a = 3 », alors « a² = 3² = 9 ».
Si « b = 2x », alors « b² = (2x)² = 4x² ».
Plusieurs Variables
Il est possible que les termes « a » et/ou « b » soient composés d’une ou plusieurs variables. Dans ce cas, on élève l’ensemble de ces variables au carré lorsqu’on applique la formule de l’identité remarquable.
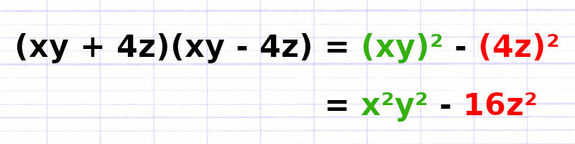
Si « a = xy », alors « a² = (xy)² = x²y² ».
Si « b = 4z », alors « b² = (4z)² = 16z² ».
Astuce
L’identité remarquable « (a + b)(a - b) = a² - b² » peut s’avérer très utile pour effectuer des calculs mentaux rapidement. Elle permet de transformer certains produits en une différence de carrés, ce qui est parfois plus simple à calculer de tête.

« 103 × 97 » peut se transformer en « (100 + 3)(100 - 3) ».
Le produit est ainsi devenu une identité remarquable que l’on peut transformer en différence de deux carrés.