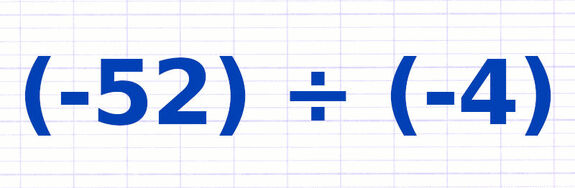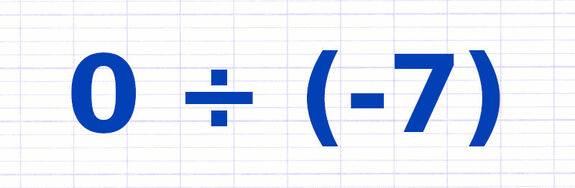Diviser des Nombres Relatifs
Théorie
La division de nombres relatifs consiste à diviser des valeurs pouvant être positives ou négatives. Cette division s’effectue en appliquant la règle des signes.
Exemple
Comment diviser ces nombres relatifs ?
Déterminer le Signe du Quotient
La 1re étape est de déterminer le signe (positif ou négatif) du quotient (résultat de la division). Le signe du quotient de 2 nombres relatifs est :
- Positif si les 2 nombres ont des signes identiques (+/+ ou -/-).
- Négatif si les 2 nombres ont des signes différents (+/- ou -/+).
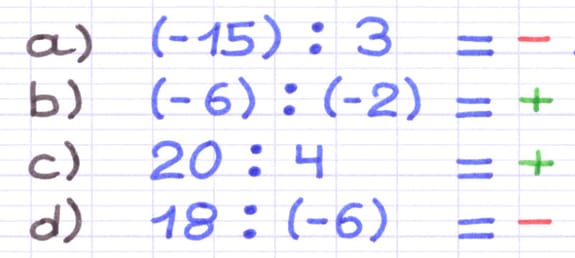
Un nombre négatif divisé par un nombre positif donne un résultat négatif.
Un nombre négatif divisé par un nombre négatif donne un résultat positif.
Un nombre positif divisé par un nombre positif donne un résultat positif.
Un nombre positif divisé par un nombre négatif donne un résultat négatif.
Effectuer la Division
Le signe du quotient étant déjà déterminé, on peut désormais effectuer les calculs comme si les signes n’existaient pas. La 2e étape est de diviser les nombres relatifs sans prendre en considération leur signe. Le résultat de la division se note derrière le signe trouvé à l’étape précédente.
Division de nombres relatifs.
Un nombre sans signe devant lui est considéré comme positif. Il n’est donc pas obligatoire de noter le signe "+" devant un nombre positif.
3 et 5 sont des nombres positifs.
-3 et -5 sont des nombres négatifs.
Écriture fractionnaire
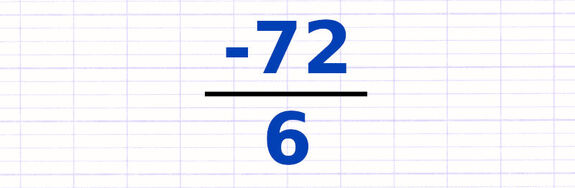
La division de 2 nombres relatifs se présente parfois sous une écriture fractionnaire. Le quotient d’une fraction s’obtient en divisant le numérateur par le dénominateur. La division s’effectue normalement, en suivant les 2 étapes précédentes.
Une fraction est une division du numérateur par le dénominateur.
Quiz
Question 1
Quel est le quotient de ces deux nombres relatifs ?
Question 2
Quel est le quotient de ces deux nombres relatifs ?
Question 3
Quel est le quotient de ces deux nombres relatifs ?