Placer une Fraction sur une Demi-Droite Graduée
Théorie
La position d’une fraction sur une demi-droite dépend de la graduation de la demi-droite. La graduation est l’ensemble des petits traits tout au long de la demi-droite.
Exemple
Comment placer la fraction 7/4 sur cette demi-droite graduée ?
Repérer une Unité de Graduation
La 1re étape est de repérer une unité de graduation sur la demi-droite. L’unité de graduation est l’espace qui sépare 2 nombres entiers consécutifs. 2 nombres entiers sont consécutifs si on passe d’un nombre à l’autre en ajoutant 1 (5 et 6 sont consécutifs, car 5 + 1 = 6).
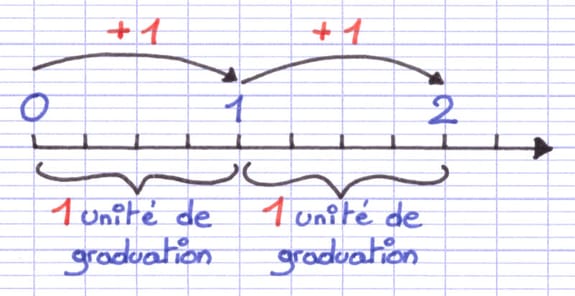
L’espace entre 0 et 1 est une unité de graduation (0 + 1 = 1).
L’espace entre 1 et 2 est une unité de graduation (1 + 1 = 2).
Compter les Traits d’une Unité
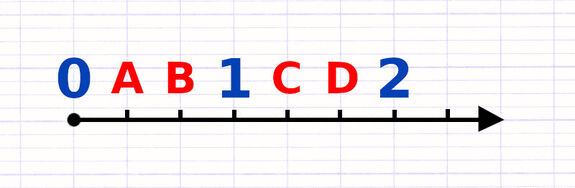
On compte ensuite le nombre de petits traits d’une unité de graduation. Pour cela, on imagine une mignonne petite sauterelle positionnée au début de l’unité de graduation. La petite sauterelle se déplace sur la demi-droite graduée en sautant d’un petit trait à l’autre. Sur combien de petits traits la sauterelle doit-elle sauter pour atteindre la fin de l’unité de graduation ?
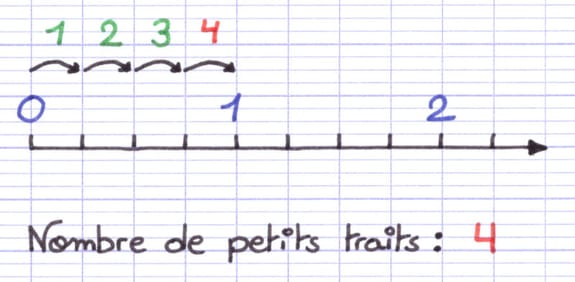
L’unité de graduation est composée de 4 petits traits.
Associer un Trait à une Fraction
L’étape suivante consiste à déterminer la fraction associée au déplacement d’un petit trait. On sait déjà qu’en se déplaçant d’une unité de graduation, on ajoute 1. La question est maintenant de savoir quelle fraction ajouter lorsqu’on se déplace d’un petit trait.
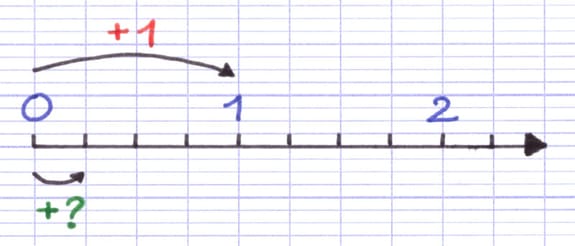
La distance d’un petit trait à l’autre est 4 fois plus petite que celle pour parcourir 1 unité de graduation.
Grâce à la règle de 3, il est possible de trouver la fraction associée au déplacement d’un petit trait.
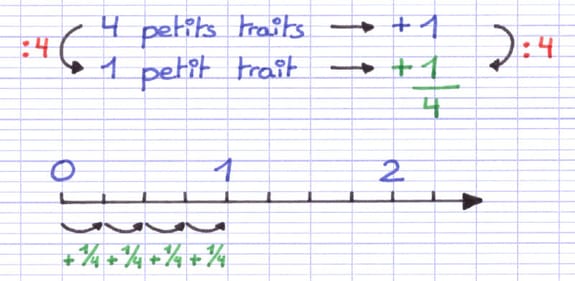
Pour se déplacer de 4 petits traits (1 unité de graduation), on ajoute 1. Pour se déplacer de 1 petit trait, on ajoute 1/4 (la distance est divisée par 4).
Placer la Fraction
La dernière étape est de placer la fraction sur la demi-droite graduée. En connaissant la fraction associée au déplacement d’un petit trait, on peut déterminer facilement les fractions associées à chacun des traits de la demi-droite graduée.
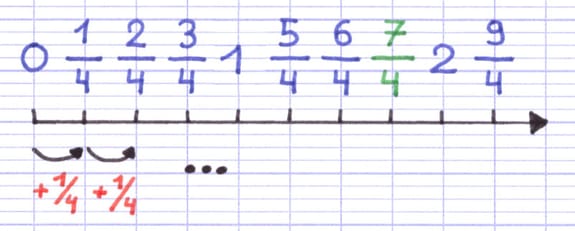
À partir de 0, on se déplace de 7 petits traits pour atteindre la fraction 7/4. À partir de 1 (ou 4/4), on se déplace de 3 petits traits pour atteindre la fraction 7/4.
Quiz
Question 1
De combien de carreaux est constituée l’unité de graduation de cette demi-droite graduée ?
Question 2
Quelle fraction est associée au déplacement d’un petit trait sur cette demi-droite graduée ?
Question 3
Quelle lettre est associée à la fraction 5/3 sur cette demi-droite graduée ?