Placer des Nombres Décimaux sur une Demi-Droite Graduée
Théorie
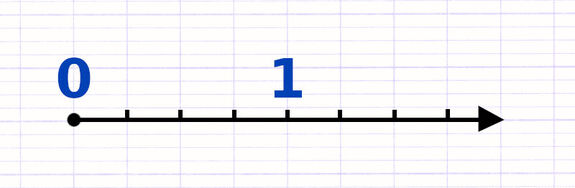
Une demi-droite graduée possède une origine (point de départ) et une graduation (petits traits). La position d’un nombre décimal sur une demi-droite dépend de sa graduation. Il est important de savoir placer des nombres entiers sur une demi-droite graduée avant de s’aventurer plus loin.
Exemple
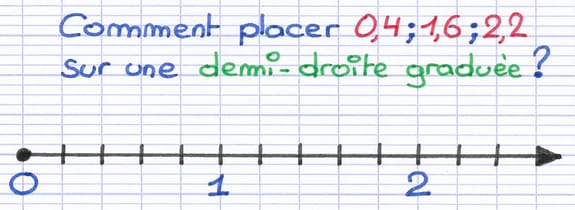
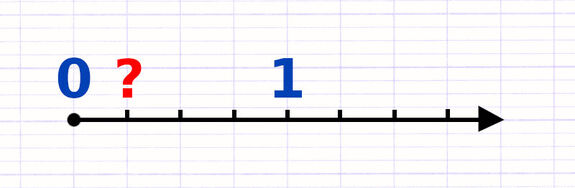
Comment placer ces nombres décimaux sur la demi-droite graduée ?
Repérer l’Unité de Graduation
La 1re étape est de repérer l’unité de graduation de la demi-droite graduée. L’unité de graduation correspond à la distance entre 2 nombres entiers consécutifs. Cette unité de graduation est identique (même longueur) partout sur l’axe gradué.
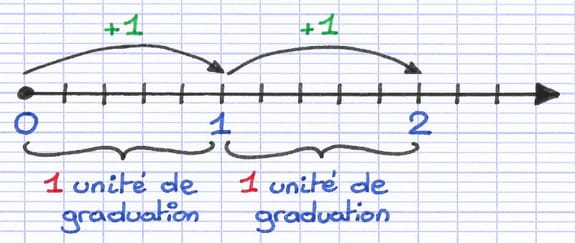
Une unité de graduation sépare les nombres entiers consécutifs 0 et 1. Une unité de graduation identique sépare les nombres entiers consécutifs 1 et 2.
Compter les Portions d’une Unité
Les petits traits de la demi-droite graduée coupent l’unité de graduation en plusieurs morceaux. L’étape suivante consiste à compter le nombre de portions qui compose l’unité de graduation.

L’unité de graduation est divisée en 5 portions.
Trouver la Valeur d’un Trait
Le déplacement d’une unité de graduation correspond à une augmentation de 1 (+1). On cherche maintenant à déterminer l’augmentation correspondant au déplacement d’un petit trait.
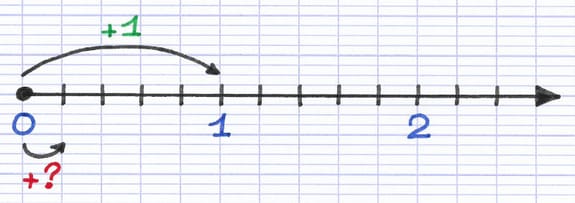
Chaque déplacement d’un trait sur la demi-droite graduée est associé à une valeur.
Pour le découvrir, on divise le chiffre 1 par le nombre de portions de l’unité de graduation (étape 2). Le résultat de cette division décimale est la valeur associée au déplacement d’un trait.
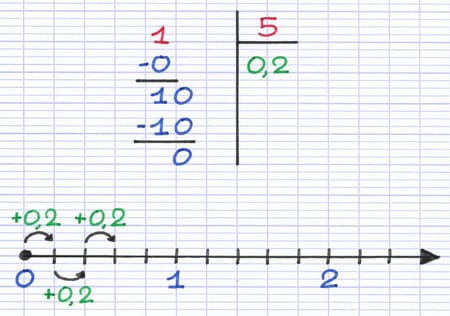
La division décimale de 1 par 5 est égale à 0,2. Le déplacement d’un trait correspond à une augmentation de 0,2.
Placer les Nombres Décimaux
Chaque déplacement d’un trait sur la demi-droite graduée est associé à la même augmentation (+0,2). Pour placer les différents nombres décimaux, il suffit donc, à partir d’un nombre entier, d’ajouter cette valeur à chaque déplacement d’un trait.
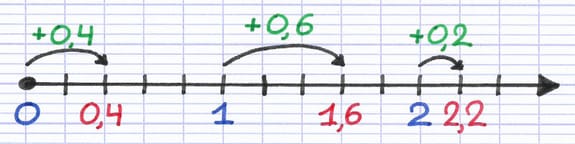
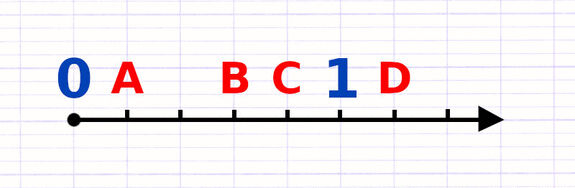
Chaque nombre décimal a une position précise sur la demi-droite graduée.
0 + 0,2 + 0,2 = 0,4.
1 + 0,2 + 0,2 + 0,2 = 1,6.
2 + 0,2 = 2,2.