Placer des Nombres Relatifs sur une Droite Graduée
Théorie
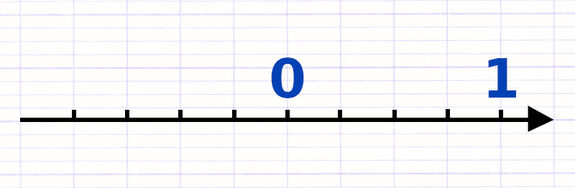
Une droite graduée possède une graduation (petits traits) sur laquelle on peut placer des nombres relatifs La position d’un nombre relatif sur une droite graduée dépend de son signe :
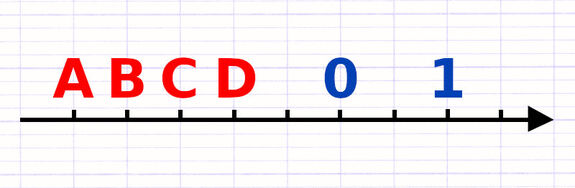
- Les nombres positifs sont placés à droite du zéro.
- Les nombres négatifs sont placés à gauche du zéro.
Exemple
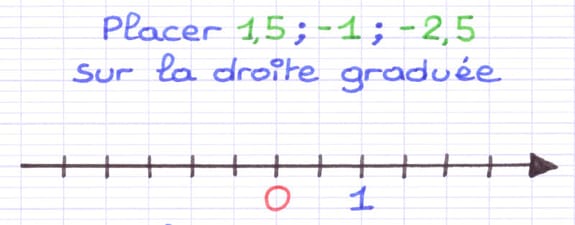
Comment placer ces nombres relatifs sur cette droite graduée ?
1. Comprendre la Graduation
L’unité de graduation de la droite est la distance entre 2 nombres entiers consécutifs. Chaque déplacement d’une unité de graduation :
- Vers la droite correspond à une augmentation de 1 (+1).
- Vers la gauche correspond à une diminution de 1 (-1).
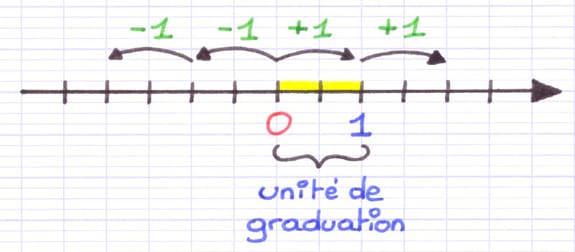
La distance entre 0 et 1 (nombres consécutifs) est l’unité de graduation de la droite. L’unité de graduation est de la même longueur partout sur la droite.
L’unité de graduation est divisée en plusieurs portions par des petits traits. Pour trouver la valeur associée au déplacement d’un trait, on divise le chiffre 1 par le nombre de portions d’une unité de graduation.
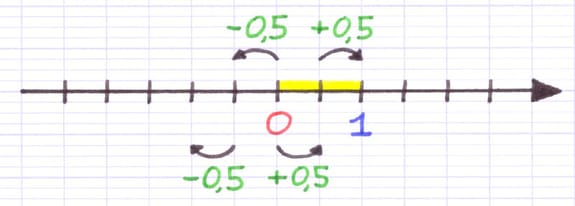
L’unité de graduation est divisée en 2 portions.
1 : 2 = 0,5
La distance entre 2 traits est donc la moitié (0,5) d’une unité de graduation.
2. Placer les Nombres Positifs
Sur la droite graduée, les nombres relatifs positifs se placent à droite du zéro. Chaque déplacement d’un trait vers la droite correspond à une augmentation de 0,5. On peut donc trouver la position d’un nombre positif en ajoutant 0,5 à chaque déplacement d’un trait vers la droite.
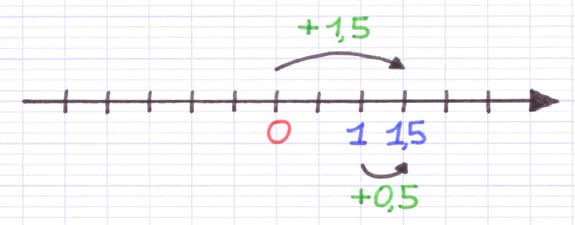
À partir de 0, on se déplace de 3 traits pour atteindre 1,5.
0 + 0,5 + 0,5 + 0,5 = 1,5
À partir de 1, on se déplace de 1 trait pour atteindre 1,5.
1 + 0,5 = 1,5
3. Placer les Nombres Négatifs
Sur la droite graduée, les nombres relatifs négatifs se placent à gauche du zéro. Chaque déplacement d’un trait vers la gauche correspond à une diminution de 0,5. On peut donc trouver la position d’un nombre négatif en retirant 0,5 à chaque déplacement d’un trait vers la gauche.
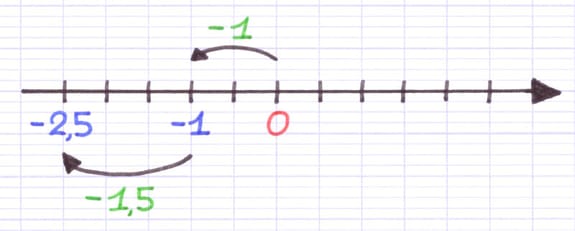
À partir de 0, on se déplace de 2 traits pour atteindre -1.
0 - 0,5 - 0,5 = -1
À partir de -1, on se déplace de 3 traits pour atteindre -2,5.
-1 - 0,5 - 0,5 - 0,5 = -2,5
Droite inversée
Une flèche à l’extrémité de la droite graduée indique le sens de déplacement. Sur une droite graduée classique (flèche vers la droite) :
- Les nombres positifs sont placés à droite du zéro.
- Les nombres négatifs sont placés à gauche du zéro.
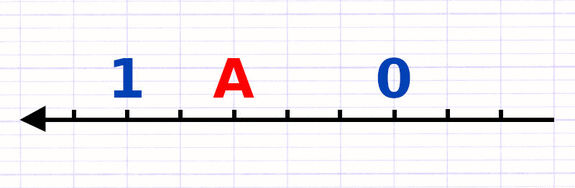
Sur une droite graduée inversée (flèche vers la gauche) :
- Les nombres positifs sont placés à gauche du zéro.
- Les nombres négatifs sont placés à droite du zéro.
Le sens de la droite graduée est inversé (flèche vers la gauche).
Exercice
Question 1
Quelle valeur est associée au déplacement d’un petit trait sur cette droite graduée ?
Question 2
Quelle lettre correspond à la position de -1,5 sur cette droite graduée ?
Question 3
Quelle valeur est associée à la lettre A sur cette droite graduée ?