Reconnaître et Décrire un Losange
Théorie
Le losange est un quadrilatère particulier qui possède 4 côtés de même longueur. Tous les losanges partagent des caractéristiques communes.
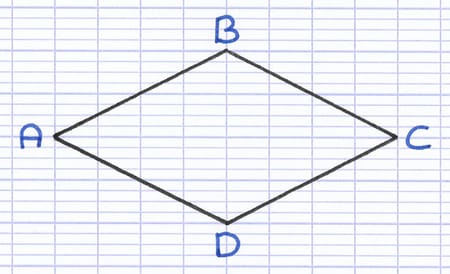
ABCD est un losange.
4 Côtés
Le losange est un quadrilatère, il possède donc 4 côtés. Ses 4 côtés ont la particularité d’être tous de la même longueur. C’est la caractéristique principale qui différencie le losange des autres quadrilatères.
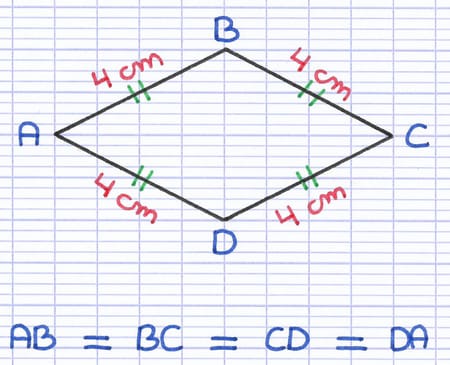
[AB], [BC], [CD] et [DA] sont les 4 côtés du losange. Ces 4 côtés ont exactement la même longueur.
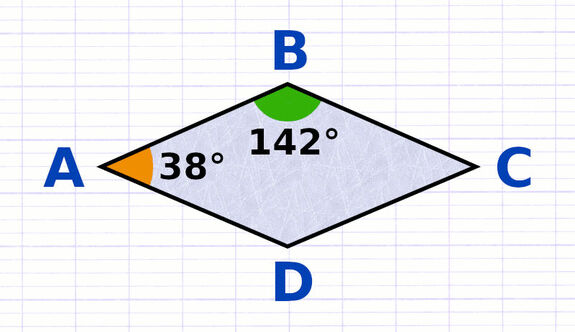
4 Angles
Le losange est un quadrilatère, il possède donc 4 angles dont la somme est égale à 360°. Les angles opposés (face à face) du losange ont la particularité d’être toujours de la même mesure. Le losange possède 2 paires d’angles opposés, donc 2 paires d’angles de même mesure. Si tous les angles d’un losange mesurent 90°, alors il s’agit d’un carré.
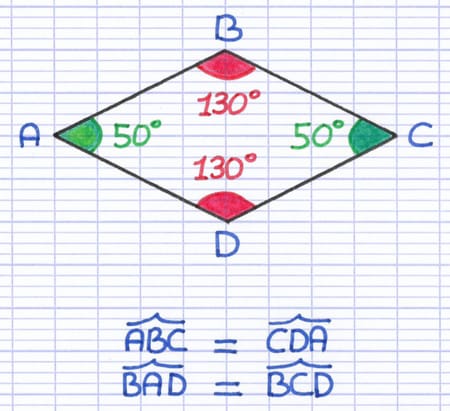
Les angles ABC et CDA sont opposés, ils mesurent chacun 130°.
Les angles BAD et BCD sont opposés, ils mesurent chacun 50°.
2 Diagonales
Le losange est un quadrilatère, il possède donc 2 diagonales qui relient les sommets opposés. Les diagonales du losange ont la particularité d’être perpendiculaires et de se couper en leur milieu.
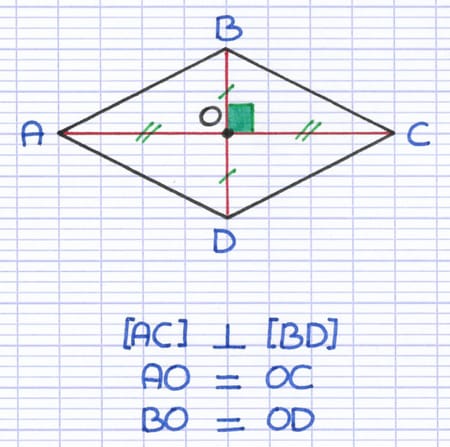
[AC] et [BD] sont les 2 diagonales perpendiculaires du losange. Leur point d’intersection (point O) est le milieu des 2 diagonales.
La longueur AO est égale à la longueur OC.
La longueur BO est égale à la longueur OD.
2 Axes de Symétrie
Un axe de symétrie est une droite qui coupe une figure géométrique en 2 parties superposables. Les 2 axes de symétrie du losange sont ses 2 diagonales. Chaque axe de symétrie coupe le losange en 2 triangles superposables.
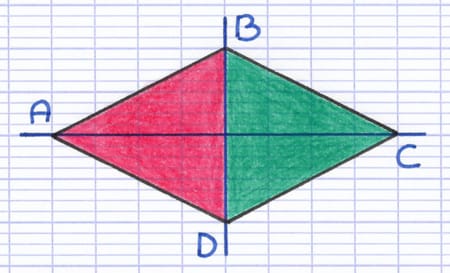
L’axe de symétrie (BD) coupe le losange en 2 triangles superposables : ABD (rouge) et CDB (vert).
L’axe de symétrie (AC) coupe le losange en 2 triangles superposables : ABC et CDA.