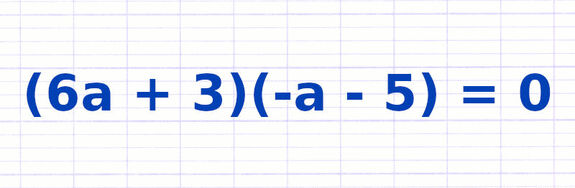Résoudre une Équation-Produit
Théorie
Un produit est le résultat d’une multiplication entre différents facteurs.
Propriété : « Pour que le produit de deux facteurs soit égal à 0 (produit nul), il suffit qu’au moins un facteur soit égal à 0 ».
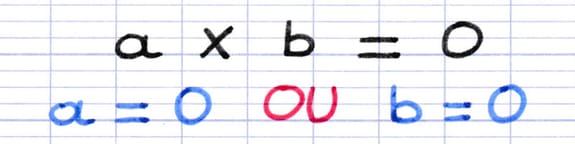
Pour que le produit de a par b soit égal à 0, il suffit que a ou b soit égal à 0.
Si a = 0, alors 0 x b = 0.
Si b = 0, alors a x 0 = 0.
Cette propriété permet de résoudre facilement une équation-produit. Une équation-produit à une équation sous la forme d’un produit égal à 0.
Exemple
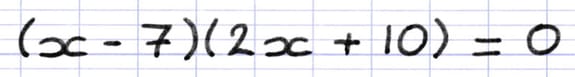
Comment résoudre cette équation-produit ?
Identifier les 2 Facteurs
Une équation-produit est composée de deux facteurs. Les facteurs sont les éléments qui sont multipliés au sein d’une multiplication. La 1re étape est d’identifier les deux facteurs de l’équation-produit.

2 parenthèses l’une à côté de l’autre est équivalent à une multiplication. Chaque parenthèse de cette équation est donc un facteur.
Trouver la 1re Solution
En-dessous de l’équation-produit, on crée une nouvelle équation dans laquelle le 1er facteur est égal à 0. On résout ensuite cette équation comme on le ferait pour n’importe quelle équation du 1er degré. La solution de cette équation est la première solution de l’équation-produit.

« x - 7 = 0 » est une équation du premier degré.
La solution de cette équation est 7.
Trouver la 2e Solution
À droite de l’équation précédente, on crée une nouvelle équation dans laquelle le 2e facteur est égal à 0. On résout ensuite cette équation du 1er degré afin de trouver la 2e solution de l’équation-produit. Les deux équations sont séparées par le mot de liaison "ou" (la solution de l’équation-produit est l’une ou l’autre des solutions des équations du 1er degré).
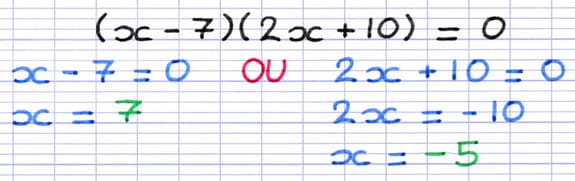
« 2x + 10 = 0 » est une équation du premier degré.
La solution de cette équation est -5.
Noter les Solutions
Les solutions trouvées aux étapes 2 et 3 sont les solutions de l’équation-produit. Ces deux solutions se notent dans des accolades sous la forme S = { solution 1 ; solution 2 }. Dans les accolades, les solutions sont classées par ordre croissant et séparées par un point-virgule.
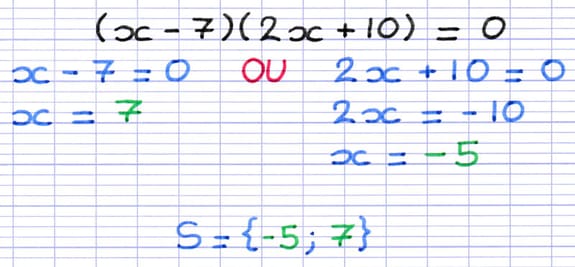
Cette équation-produit possède deux solutions : -5 ou 7.
Factorisation
Certaines équations du second degré peuvent se transformer en équation-produit grâce à la factorisation. On peut ensuite les résoudre facilement en suivant les mêmes étapes.

« 7x² - 3x » peut être factorisé en mettant en évidence le facteur commun « x ». On obtient ainsi une équation-produit.