Résoudre une Équation du Premier Degré
Théorie
Une équation est une expression littérale sous la forme d’une égalité entre 2 membres. Les 2 membres de l’équation sont séparés par le signe égal (=).
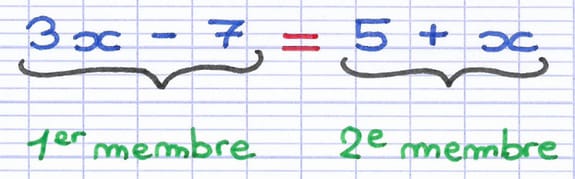
Une équation possède 2 membres : l’un à gauche du signe égal, l’autre à droite.
Chaque membre est composé d’un ou plusieurs termes. Les termes sont séparés par les signes d’addition (+) et de soustraction (-).

Chaque membre est composé de 2 termes. Cette équation possède donc un total de 4 termes.
Chaque terme appartient à une famille :
- Les termes avec "x" appartiennent à la famille "x".
- Les termes sans "x" appartiennent à la famille des termes indépendants.

2 termes sont de la famille "x" : 3x et x.
2 termes sont des termes indépendants : 7 et 5.
Une équation est toujours composée d’au moins une lettre (généralement "x") qui représente une valeur inconnue. L’objectif d’une résolution d’équation est de trouver cette valeur inconnue.
Exemple

Comment résoudre cette équation du premier degré ?
Regrouper les Inconnues
La 1re étape est de regrouper la famille "x" (les inconnues) dans le 1er membre de l’équation. Les termes avec "x" qui sont déjà dans le 1er membre ne bougent pas (ils sont au bon endroit). Par contre, les termes avec "x" du 2e membre se déplacent dans le 1er membre en respectant 2 règles :
- Un terme se déplace avec le signe à sa gauche (+ ou -).
- Le signe d’un terme change lors du passage d’un membre à l’autre (+ devient - et - devient +).
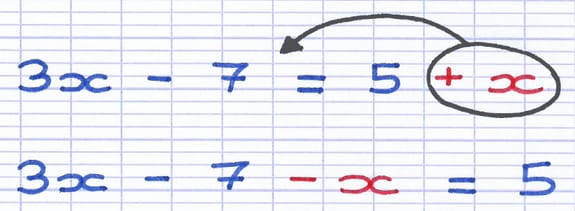
Le terme "x" se déplace vers le 1er membre. Son signe était au départ positif (+x), il devient négatif (-x). La famille des "x" est maintenant regroupée dans le 1er membre.
Cette technique de déplacement des termes au sein d’une équation repose sur un principe de résolution d’équation très important. On peut modifier l’écriture d’une équation en effectuant la même opération mathématique au sein du 1er et 2e membre de l’équation. Dans cette étape, déplacer "x" au sein du 1er terme revient à soustraire "x" des 2 membres de l’équation :
- Dans le 1er membre, on retire "x" et donc apparaît "-x".
- Dans le 2e membre, on retire également "x" et donc "x" disparaît (x - x = 0).
Regrouper les Termes Indépendants
L’étape suivante est de regrouper tous les termes indépendants au sein du 2e membre de l’équation. Les termes indépendants qui sont déjà dans le 2e membre ne bougent pas (ils sont au bon endroit). Par contre, les termes indépendants du 1er membre se déplacent dans le 2e membre en respectant les 2 mêmes règles :
- Un terme se déplace avec le signe à sa gauche (+ ou -).
- Le signe change lorsqu’il passe d’un membre à l’autre (+ devient - et - devient +).
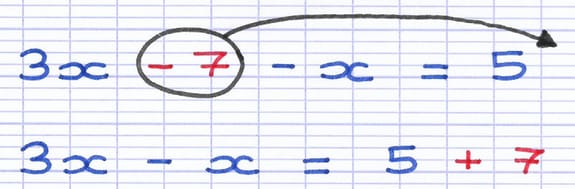
Le terme "7" se déplace vers le 2e membre. Son signe était au départ négatif (-7), il devient positif (+7). Les termes indépendants sont maintenant regroupés dans le 2e membre.
Dans cette étape, déplacer "-7" au sein du 2e terme revient à ajouter "7" au sein des 2 membres de l’équation :
- Dans le 1er membre, on ajoute "7" et donc "7" disparaît (-7 + 7 = 0).
- Dans le 2e membre, on ajoute également "7" et donc "+7" apparaît.
Réduire l’Équation
Une fois les inconnues regroupées dans le 1er membre et les termes indépendants dans le 2e membre, on passe à la réduction de l’équation. Pour réduire une équation, on additionne et soustrait les termes appartenant à une même famille :
- Dans le 1er membre, on effectue l’addition et la soustraction des termes de la famille "x".
- Dans le 2e membre, on effectue l’addition et la soustraction des termes indépendants.

Réduction du 1er membre : 3x - x = 2x.
Réduction du 2e membre : 5 + 7 = 12.
Diviser par le Coefficient
Pour trouver la valeur de l’inconnue "x", il ne reste plus qu’à diviser chaque membre de l’équation par le coefficient de "x". Le coefficient de "x" est le nombre collé à gauche de l’inconnue. L’objectif de cette division est d’isoler totalement l’inconnue au sein de l’équation afin d’obtenir "x = une valeur".

Le coefficient de "x" est 2.
Division du 1er membre : 2x / 2 = x.
Division du 2e membre : 12 / 2 = 6.
Noter la Solution de l’Équation
Lorsque l’équation est sous la forme "x = une valeur numérique", la résolution est terminée. La valeur à droite du signe égal est la valeur de l’inconnue. La solution de l’équation se note entre des accolades : "S = { valeur }".
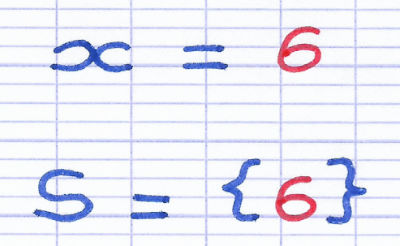
Dans cette équation, la valeur de "x" est égale à "6". Le "S" majuscule signifie "Solution".
Technique de vérification
Il est possible de vérifier facilement si la solution de l’équation est correcte. On remplace pour cela l’inconnue par la valeur trouvée, puis on effectue les opérations au sein de chaque membre. Si les 2 membres de l’équation sont égaux, alors la solution trouvée est correcte.

La vérification s’effectue en remplaçant "x" par la valeur trouvée (6). On obtient une égalité (11 = 11), la solution de l’équation est donc correcte.