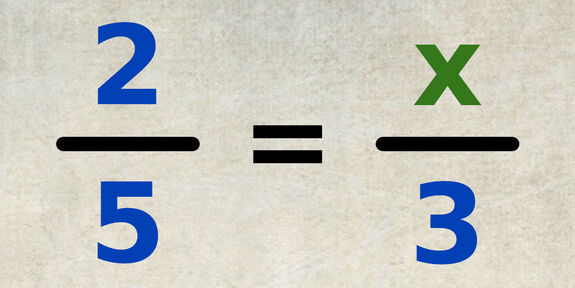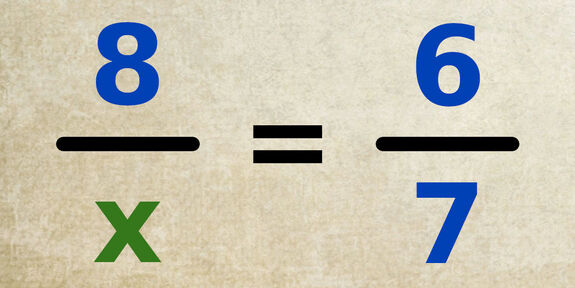Résoudre une Équation avec le Produit en Croix
Théorie
Certaines équations se présentent sous la forme d’une égalité entre deux fractions. Pour résoudre ces équations, une technique efficace consiste à utiliser le produit en croix.
Produit en croix : « Si deux fractions sont égales, alors les produits des nombres en diagonal sont égaux ».
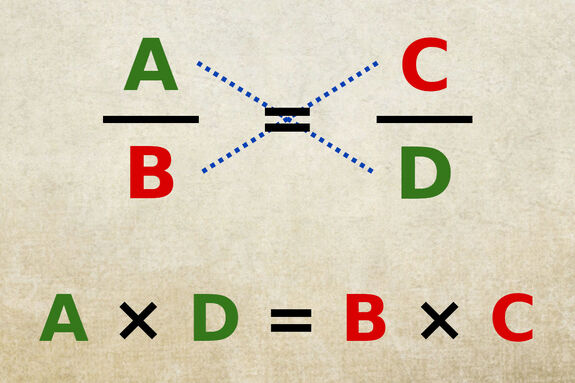
Les fractions « A/B » et « C/D » sont égales.
D’après le produit en croix, les produits des nombres en diagonal « A × D » et « B × C » sont égaux.
L’application du produit en croix transforme une égalité de fractions en égalité de produits. Il est ensuite possible d’isoler la valeur de son choix au sein de l’équation. On utilise pour cela la propriété de division des équations.
Propriété de division des équations : « Dans une équation, le membre de gauche et le membre de droite peuvent être divisés par un même nombre ».
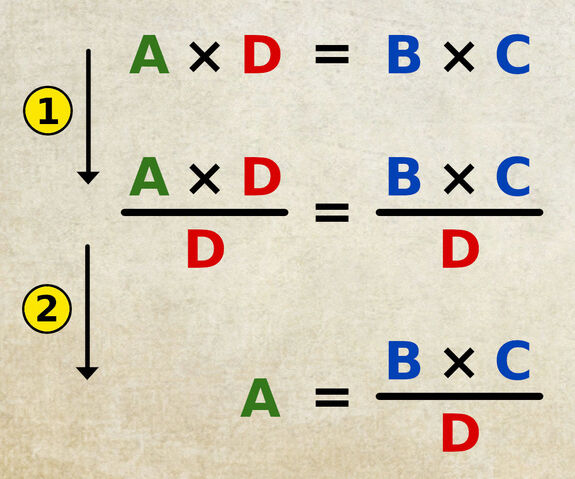
1) Le membre de gauche et le membre de droite sont divisés par « D ».
2) La valeur « A » est ainsi isolée dans le membre de gauche, car la division par « D » annule la multiplication par « D ».
Les deux opérations précédentes (produit en croix et division) peuvent être effectuées en même temps afin d’isoler une valeur plus rapidement. Il suffit pour cela d’appliquer dès le départ la propriété ci-dessous qui découle du produit en croix.
Propriété du produit en croix : « Dans une égalité de deux fractions, chaque valeur est égale au produit des valeurs sur l’autre diagonale, divisé par la valeur restante ».
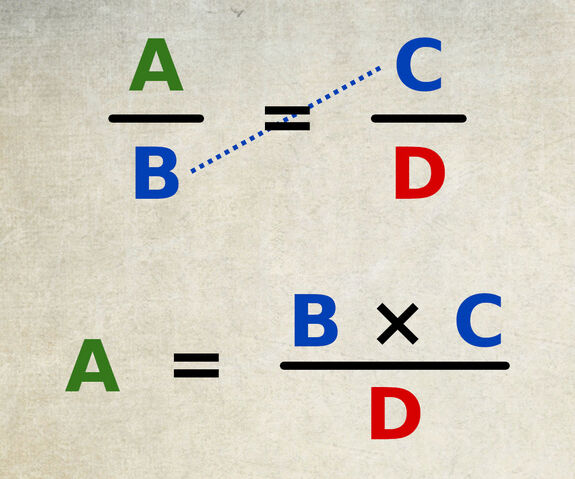
« A » est égal au produit des valeurs sur l’autre diagonale « B × C », divisé par la valeur restante « D ».
Cette propriété du produit de croix permet de résoudre facilement une équation sous la forme d’une égalité de fractions.
Exemple 1
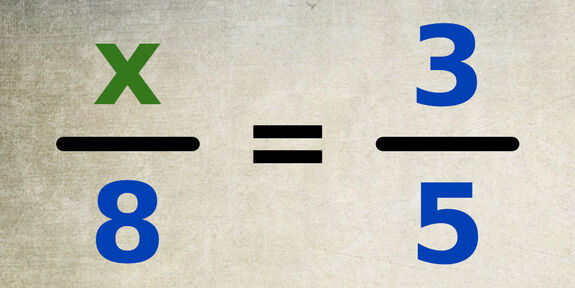
Comment résoudre cette équation dont l’inconnue est au numérateur ?
Cette équation se présente sous la forme d’une égalité entre deux fractions. L’inconnue « x » se situe au numérateur.
Résoudre une équation consiste à déterminer la valeur de l’inconnue en l’isolant au sein de l’équation. La résolution peut s’effectuer en deux étapes.
- Utiliser la propriété du produit en croix pour isoler l’inconnue.
- Effectuer les calculs pour déterminer la valeur de l’inconnue.
Propriété du produit en croix : « Dans une égalité de deux fractions, chaque valeur est égale au produit des valeurs sur l’autre diagonale, divisé par la valeur restante ».
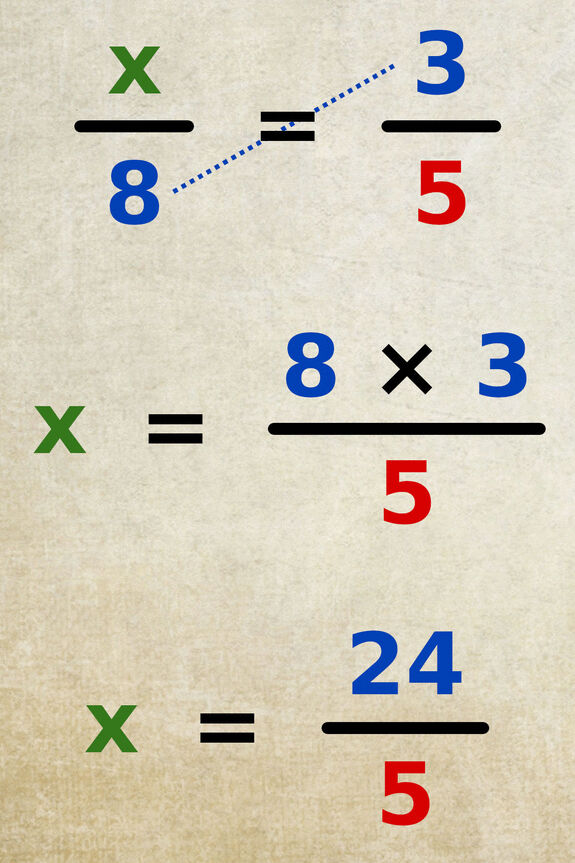
D’après le produit en croix, « x » est égal au produit des valeurs sur l’autre diagonale « 8 × 3 », divisé par la valeur restante « 5 ».
Il ne faut pas oublier de simplifier, si possible, la fraction obtenue. Dans cet exemple, la fraction « 24/5 » est irréductible, il s’agit de la solution de l’équation.
Exemple 2
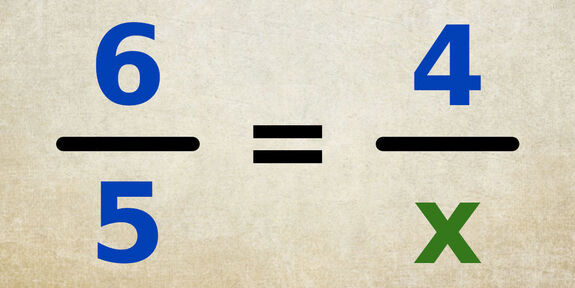
Comment résoudre cette équation dont l’inconnue est au dénominateur ?
Au sein d’une égalité de fractions, l’inconnue est parfois située au dénominateur. Les deux étapes pour résoudre ces équations sont identiques, quelle que soit la position de l’inconnue.
- Utiliser la propriété du produit en croix pour isoler l’inconnue.
- Effectuer les calculs pour déterminer la valeur de l’inconnue.
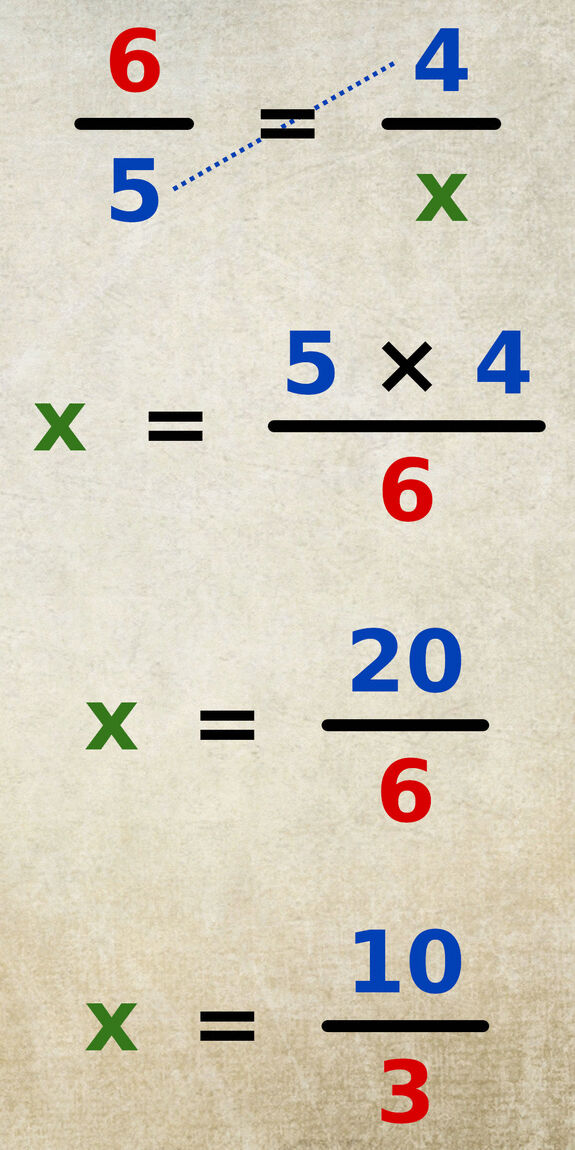
D’après le produit en croix, « x » est égal au produit des valeurs sur l’autre diagonale « 5 × 4 », divisé par la valeur restante « 6 ».
Dans cet exemple, il est nécessaire de simplifier la solution obtenue afin d’obtenir une fraction irréductible. La solution de l’équation est la fraction « 10/3 ».
Exemple 3
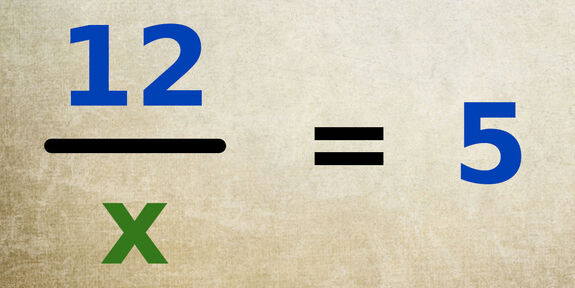
Comment résoudre cette équation de la forme d’une égalité entre un nombre entier et une fraction ?
Le produit en croix permet également de résoudre une égalité entre un nombre entier et une fraction. Pour cela, on commence par transformer le nombre entier en fraction en appliquant la propriété ci-dessous.
Propriété : « Tout nombre entier peut s’écrire sous la forme d’une fraction dont le dénominateur est 1 ».
Une fois le nombre entier transformé en fraction, on se retrouve face à une égalité de fractions. Il est désormais possible d’utiliser le produit en croix pour résoudre l’équation.
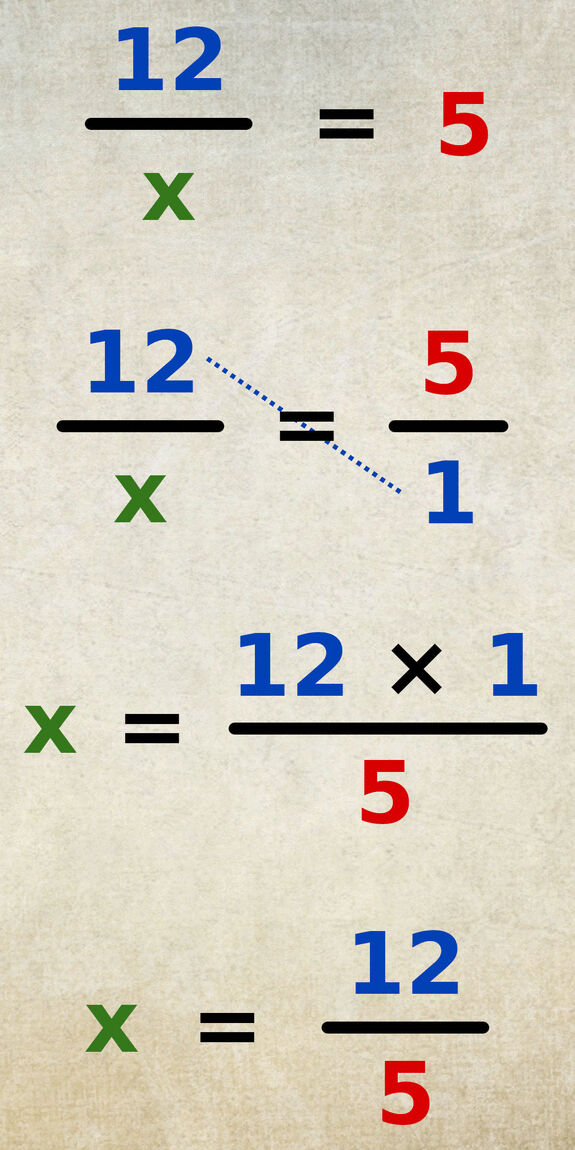
Le nombre entier « 5 » est équivalent à la fraction « 5/1 ».
« x » est égal au produit des valeurs sur l’autre diagonale « 12 × 1 », divisé par la valeur restante « 5 ».