Simplifier une Puissance avec une Racine Carrée
Théorie
Racine et puissance sont intimement liées. La racine carrée est l’inverse de la puissance carrée.
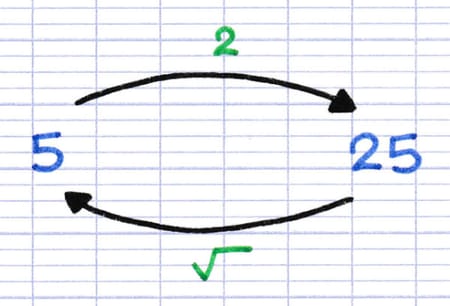
52 = 25
√25 = 5
Racine et puissance peuvent se simplifier mutuellement :
- La racine carrée d’un nombre élevé au carré est égale à ce nombre.
- Le carré de la racine carrée d’un nombre est égal à ce nombre.
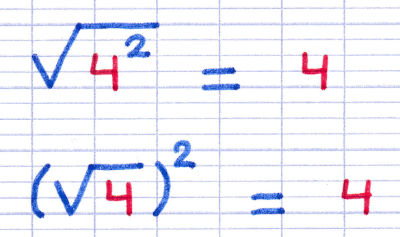
La racine carrée de 42 est égale à 4.
Le carré de la racine carrée de 4 est égal à 4.
Exemple

Comment calculer la racine carrée de 62 ?
Dans cet exemple, le radicande (nombre à l’intérieur du radical) est un nombre élevé au carré. Le calcul d’une racine carrée s’effectue en répondant à la question suivante : "Quel nombre élevé au carré est égal au radicande ?". Lorsque le radicande est une puissance carrée, la réponse est facile à trouver.

"Quel nombre élevé au carré est égal à 62 ?"
6 élevé au carré est égal à 62.
La racine carrée de 62 est donc 6.
On peut donc en déduire que la racine carrée d’un nombre élevé au carré est égale à ce nombre. La racine et l’exposant se simplifient mutuellement.

Simplification : Racine carrée et puissance carrée se neutralisent mutuellement.
Exemple
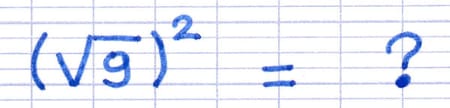
Comment calculer le carré de la racine carrée de 9 ?
Dans cet exemple, la racine carrée est elle-même élevée au carré. Selon l’ordre de priorité des opérations (PEMDAS), on effectue en priorité les calculs au sein des parenthèses. La 1re étape est donc de calculer la racine carrée à l’intérieur de la parenthèse.

"Quel nombre au carré est égal à 9 ?"
32 = 9.
La racine carrée de 9 est donc égale à 3.
L’étape suivante consiste à calculer la puissance. Un nombre élevé au carré se calcule en multipliant le nombre par lui-même. On peut alors constater que le résultat obtenu est le radicande de départ.
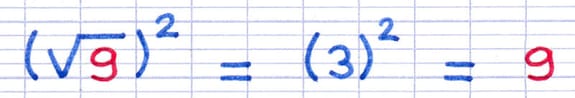
32 = 3 x 3 = 9.
On peut en déduire que le carré de la racine carrée d’un nombre est égal à ce nombre. L’exposant et la racine se simplifient mutuellement.

Simplification : Puissance carrée et racine carrée se neutralisent mutuellement.

