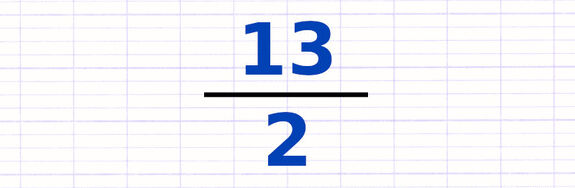
Trouver l’Inverse d’un Nombre ou d’une Fraction
Théorie
L’inversion est une transformation qui consiste à inverser le numérateur et le dénominateur d’une fraction. Pour inverser un nombre, il faut donc au préalable le visualiser sous la forme d’une fraction.
Inverser une Fraction
Pour inverser une fraction, il suffit de la retourner. Le numérateur devient le dénominateur, tandis que le dénominateur devient le numérateur.
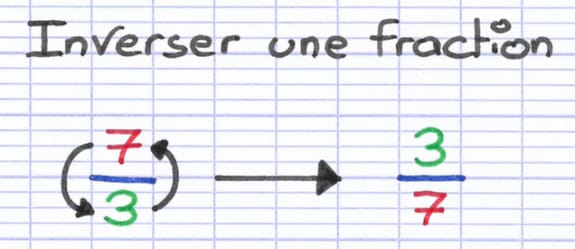
3/7 est l’inverse de la fraction 7/3.
Inverser un Nombre Entier
Tout nombre entier peut s’écrire sous forme d’une fraction dont le dénominateur est le chiffre 1. En visualisant le nombre sous la forme d’une fraction, il est ensuite facile de trouver son inverse.
1/12 est l’inverse du nombre entier 12.
Inverser un Nombre Décimal
Tout nombre décimal peut s’écrire sous forme d’une fraction décimale. Pour inverser un nombre décimal, on commence donc par le transformer en fraction décimale. La fraction est ensuite retournée afin d’obtenir son inverse.
10/89 est l’inverse du nombre décimal 8,9.
Inverser Zéro
Il est impossible d’inverser zéro, l’inverse de zéro n’existe donc pas. Si on retourne la fraction, le zéro apparaît au dénominateur... Or le dénominateur d’une fraction ne peut jamais être égal à 0 !
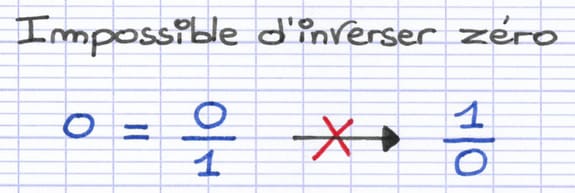
Il est impossible d’inverser le chiffre 0.
Propriétés
Propriété : "Si A est l’inverse de B, alors B est l’inverse de A".
L’inversion est réciproque, elle fonctionne dans les deux sens.
L’inversion est réciproque.
Propriété : "Deux nombres sont inverses si leur produit est égal à 1".
Cette propriété peut être utilisée afin de vérifier qu’un nombre est l’inverse d’un autre.
2/3 est l’inverse de 3/2.
0,4 n’est pas l’inverse de 4.
2 est l’inverse de 0,5.
Quiz
Question 1
Quel est l’inverse de cette fraction ?
Question 2
Laquelle de ces propositions est fausse ?
Question 3
Quel est l’inverse de ce nombre décimal ?