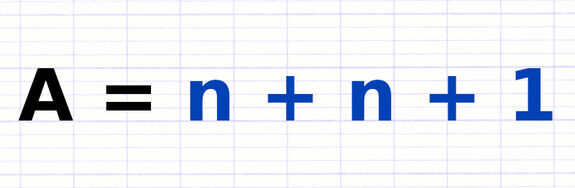Démontrer que la Somme de 2 Entiers Consécutifs est Impaire
Théorie
En mathématiques, démontrer une proposition consiste à prouver qu’elle est vraie en utilisant un raisonnement logique. La démonstration que la somme de 2 nombres entiers consécutifs est impaire s’effectue en 3 étapes.
1. Écrire la Somme de 2 Entiers Consécutifs
La somme de 2 entiers consécutifs peut s’écrire sous la forme d’une expression littérale. Si x est un nombre entier, alors x + 1 est le nombre suivant. x et x + 1 sont donc 2 entiers consécutifs. En plaçant le signe de l’addition entre les deux, on obtient la somme de 2 entiers consécutifs.
x + x + 1 est la somme de deux nombres entiers consécutifs.
2. Réduire l'Expression Littérale
L’expression littérale de la somme de 2 entiers consécutifs peut être réduite. La réduction s’effectue en additionnant les termes de la famille de l’inconnue x.
2x + 1 est la forme réduite de la somme de deux entiers consécutifs.
3. Reconnaître un Nombre Impair
Le résultat obtenu est l’expression littérale d’un nombre impair. Si x est un nombre entier, 2x est forcément un nombre pair (car c’est le produit d’un nombre entier par 2). Donc 2x + 1 est obligatoirement un nombre impair (on obtient toujours un nombre impair en ajoutant 1 à un nombre pair).
La somme de 2 entiers consécutifs est donc égale à un nombre impair, la démonstration est terminée.
Démonstration que la somme de deux entiers consécutifs est impaire.
Exercice
Question 1
Au sein de cette expression littérale, quels sont les deux termes désignant les deux nombres entiers consécutifs ?
Question 2
Quelle proposition désigne la réduction de l’expression littérale B ?
Question 3
Quelle doit être la valeur de b pour que l’expression littérale E désigne le nombre impair 63 ?