Utiliser la Somme des Angles d’un Triangle
Théorie
Propriété : "La somme des mesures des angles d’un triangle est toujours égale à 180°".
Cette propriété est valable quelle que soit la nature du triangle (quelconque, rectangle, isocèle ou équilatéral).
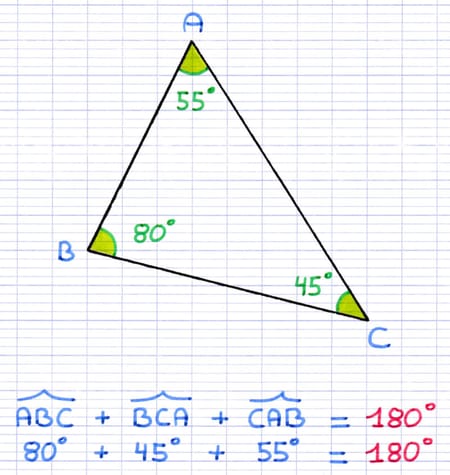
La somme des angles de ce triangle est égale à 180°.
Grâce à cette propriété, il est possible de calculer la mesure de certains angles au sein d’un triangle.
Triangle Quelconque
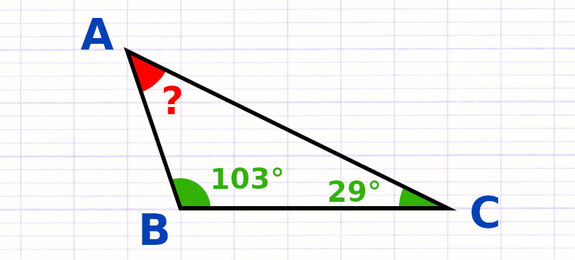
Tout triangle, quelle que soit sa nature, possède exactement 3 angles. Si on connait la mesure de deux angles, on peut calculer la mesure du 3e angle. Il suffit de trouver la mesure manquante pour que la somme des 3 angles soit égale à 180°.
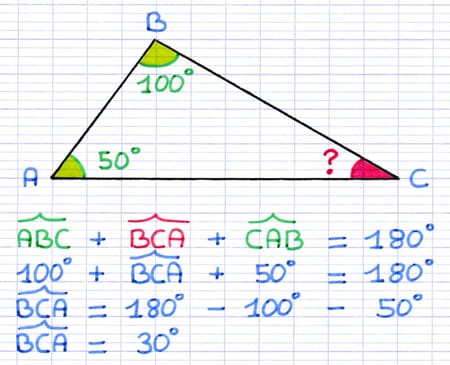
Le 3e angle doit mesurer 30° pour que la somme des angles soit égale à 180°.
100° + 30° + 50° = 180°
Triangle Rectangle
Le triangle rectangle possède un angle droit (90°) et 2 angles aigus. La somme des 2 angles aigus est donc forcément égale à 90°. Si on connait la mesure d’un angle aigu, on peut dès lors calculer la mesure de l’autre angle aigu. Il suffit de trouver la mesure manquante pour que la somme des 2 angles aigus soit égale à 90°.
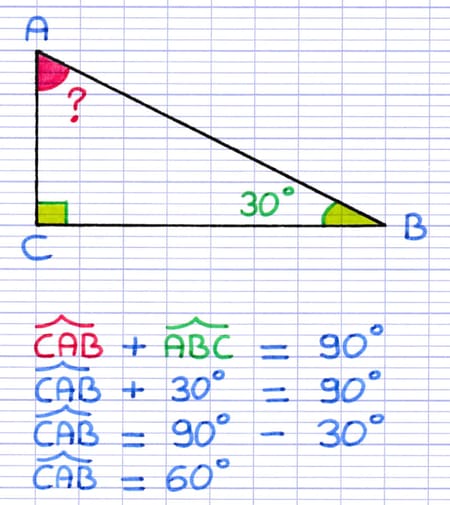
Le 2e angle aigu doit mesurer 60° pour que la somme des angles aigus soit égale à 90°.
60° + 30° + 90° = 180°
Triangle Isocèle
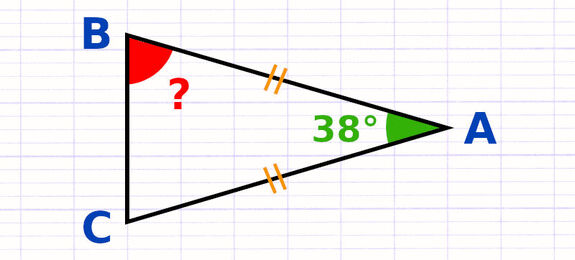
Les 2 angles à la base d’un triangle isocèle ont la même mesure. Si on connait l’angle du sommet principal, on peut calculer la mesure des 2 angles à la base. Il suffit de soustraire de 180° la mesure de l’angle du sommet principal, puis de diviser le résultat par 2.
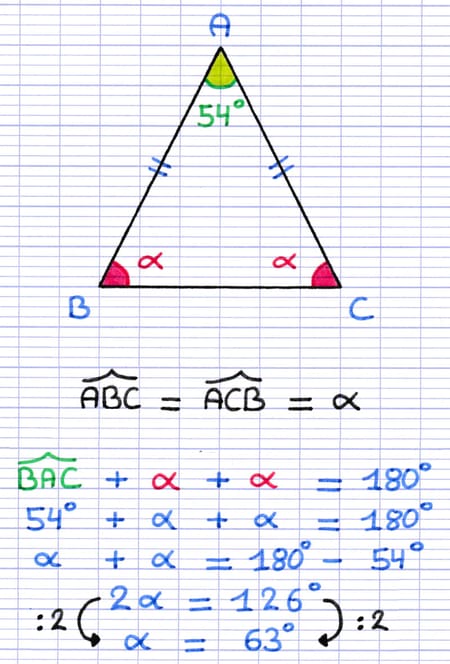
Dans ce triangle isocèle, A est le sommet principal et [BC] est la base. Chaque angle à la base doit mesurer 63° pour que la somme des angles soit égale à 180°.
54° + 63° + 63° = 180°
Triangle Équilatéral
Le triangle équilatéral possède 3 angles de même mesure. Puisque la somme des 3 angles identiques est égale à 180°, chaque angle mesure forcément 60°.
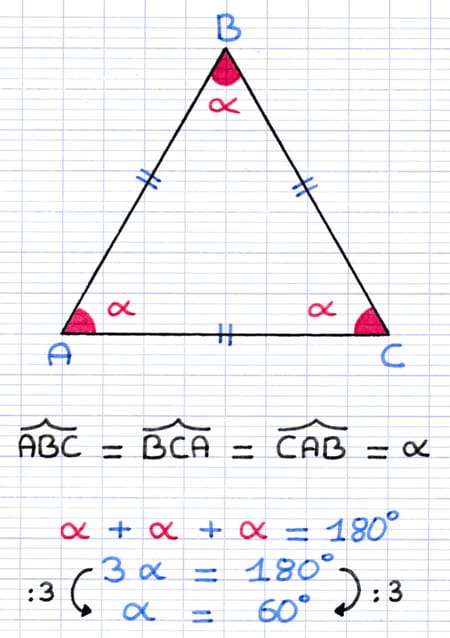
Chaque angle du triangle équilatéral mesure 60°.
60° + 60° + 60° = 180°