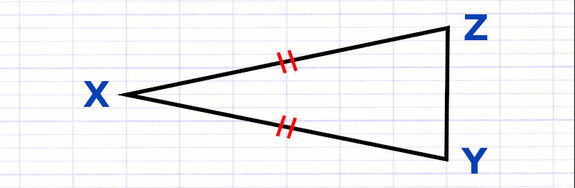
Reconnaître et Décrire un Triangle Isocèle
Théorie
Un triangle est un polygone à 3 côtés. Il existe 3 triangles particuliers :
- Le triangle rectangle (1 angle droit).
- Le triangle isocèle (2 côtés égaux).
- Le triangle équilatéral (3 côtés égaux).
Le triangle isocèle possède 2 côtés de même longueur, 2 angles de même mesure, 1 sommet principal, 1 base et 1 axe de symétrie.
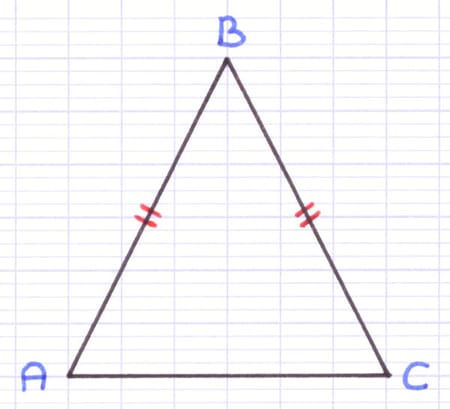
Le triangle ABC est un triangle isocèle en B.
Côtés
La caractéristique principale du triangle isocèle est qu’il possède 2 côtés de même longueur. Les 2 côtés de même longueur sont généralement indiqués par 2 petites barres identiques.
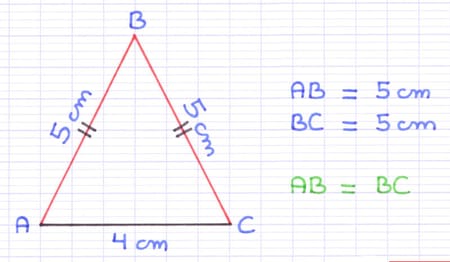
2 petites barres sur les côtés [AB] et [BC] indiquent qu’ils ont la même longueur (5 cm).
Sommet Principal
Le sommet principal du triangle isocèle est le sommet commun aux 2 côtés de même longueur. Lorsqu’on nomme un triangle isocèle, on précise généralement son sommet principal. Grâce à cette information, il est possible d’identifier les 2 côtés de même longueur.
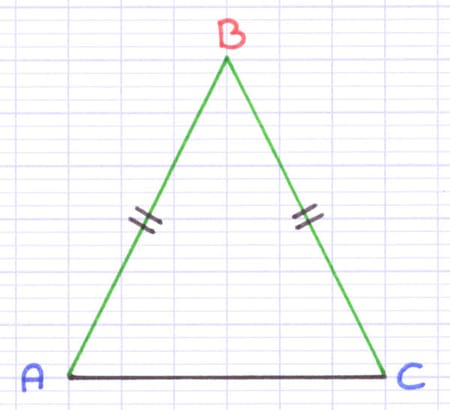
Le sommet principal B est commun aux 2 côtés de même longueur. On dit que le triangle ABC est isocèle en B. On sait alors que les 2 côtés issus du sommet B, [BA] et [BC], sont de même longueur.
Base
La base du triangle isocèle est le côté opposé au sommet principal (en face). La base est le seul côté qui ne touche pas le sommet principal.
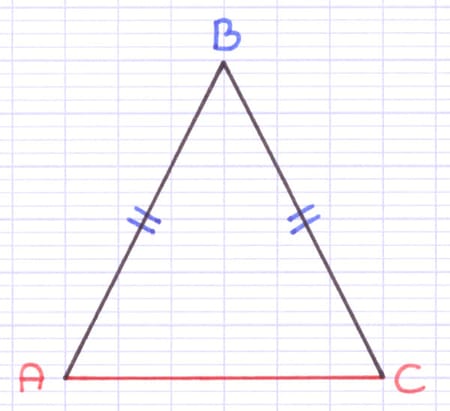
[AC] est le côté opposé au sommet principal B. La base du triangle isocèle est donc [AC].
Angles
Le triangle isocèle possède également 2 angles de même mesure. Ces 2 angles sont situés à la base du triangle.
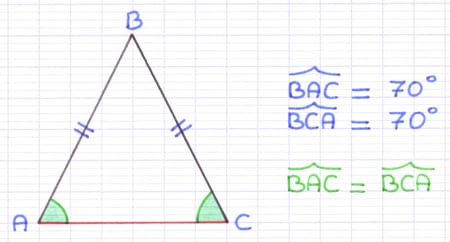
Il y a 2 angles à la base du triangle isocèle : BAC et BCA. Ces 2 angles ont la même mesure (70°).
Axe de Symétrie
Un axe de symétrie est une droite qui coupe une figure géométrique en 2 parties superposables. Le triangle isocèle possède 1 axe de symétrie. L’axe de symétrie est la médiatrice de la base du triangle (elle coupe perpendiculairement la base en son milieu).
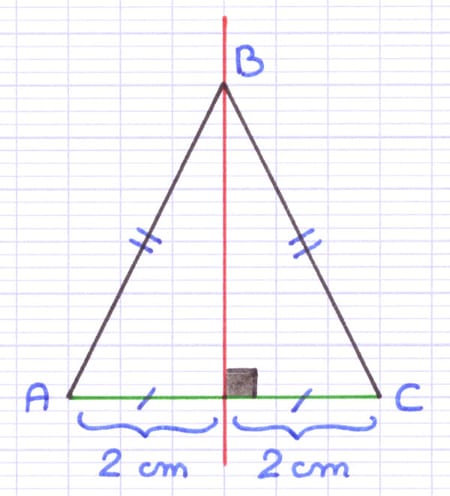
La droite rouge est l’axe de symétrie du triangle isocèle. L’axe de symétrie passe perpendiculairement par le milieu de la base.
Exercices
Question 1
Quels sont les deux côtés égaux de ce triangle isocèle ?
Question 2
Combien d’angle(s) de même mesure possède le triangle isocèle ?
Question 3
Quel est le sommet principal de ce triangle isocèle ?