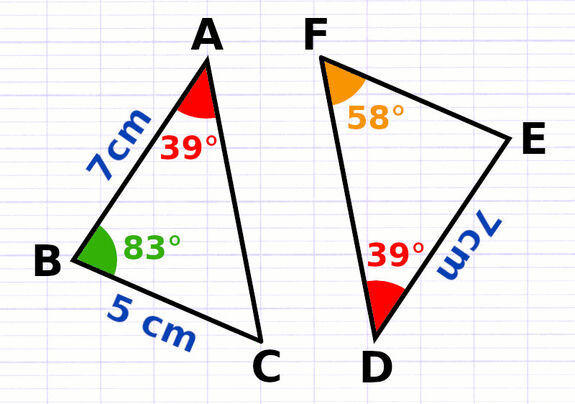
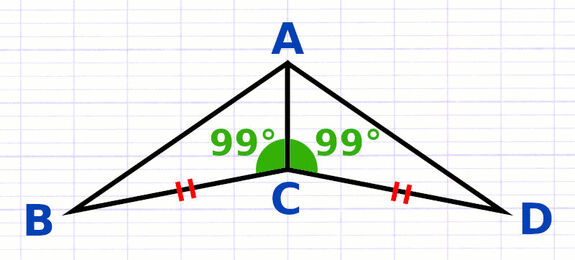
Démontrer que 2 Triangles sont Égaux

🎯

Questions validées : 0 / 3

Accédez aux exercices

Théorie

La démonstration que deux triangles sont égaux s’effectue à partir de l’un des 3 cas d’égalité des triangles.

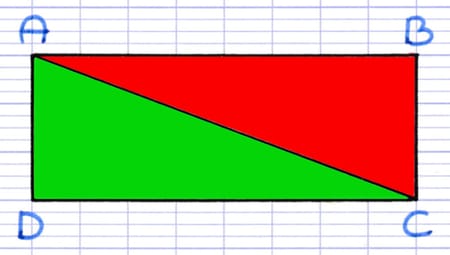
Démontrer que des triangles sont égaux — Au sein du rectangle ABCD, comment démontrer que les triangles ABC et CDA sont égaux ?

3 Côtés (CCC)

On peut démontrer que deux triangles sont égaux en indiquant qu’ils ont 3 paires de côtés de même longueur. La démonstration commence en cherchant 1 paire de côtés de même longueur. Cette 1^ère paire de côtés apparait facilement puisque les deux triangles ont un côté commun.

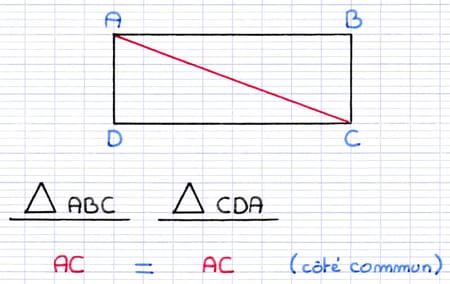
2 triangles ayant une paire de côtés de même longueur — Le côté [AC] est commun aux 2 triangles. Il s’agit de la 1^ère paire de côtés de même longueur.

On part ensuite à la recherche de 2 autres paires de côtés de même longueur. Ces 2 paires de côtés sont les paires de côtés opposés du rectangle ABCD. Dans un rectangle, les côtés opposés ont toujours la même longueur.

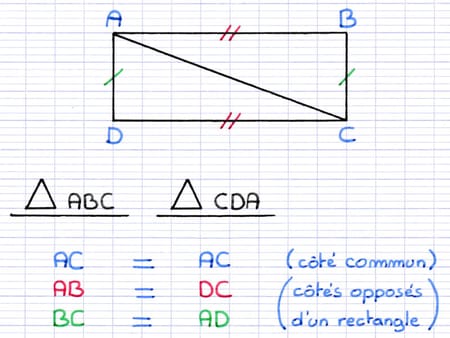
Démonstration que 2 triangles sont égaux avec le cas d’égalité CCC — [AB] et [DC] sont 2 côtés opposés d’un rectangle, ils ont donc la même longueur.

[BC] et [AD] sont 2 côtés opposés d’un rectangle, ils ont donc la même longueur.

Il s’agit des 2 autres paires de côtés de même longueur.

Les triangles ABC et CDA ont 3 paires de côtés de même longueur. On peut donc conclure que, d’après le cas d’égalité CCC, ces deux triangles sont égaux.

1 Angle entre 2 Côtés (CAC)

On peut démontrer que deux triangles sont égaux en indiquant qu’ils ont 1 paire d’angles de même mesure entre 2 paires de côtés de même longueur. La démonstration commence en cherchant 1 paire d’angles de même mesure. Cette paire d’angles apparait facilement puisque tous les angles d’un rectangle mesurent 90°.

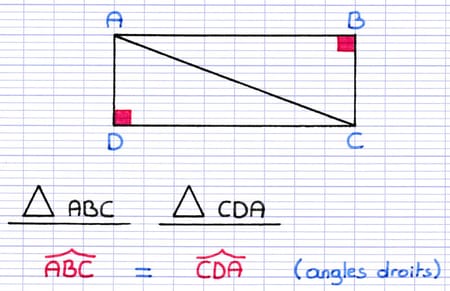
2 triangles ayant une paire d’angles de même mesure — ABC et CDA sont 2 angles droits d’un rectangle, ils ont donc la même mesure.

Il s’agit d’une paire d’angles de même mesure.

Pour compléter la démonstration, on doit indiquer que cette paire d’angles est entre 2 paires de côtés de même longueur. Ces 2 paires de côtés sont les paires de côtés opposés du rectangle ABCD. Dans un rectangle, les côtés opposés ont toujours la même longueur.

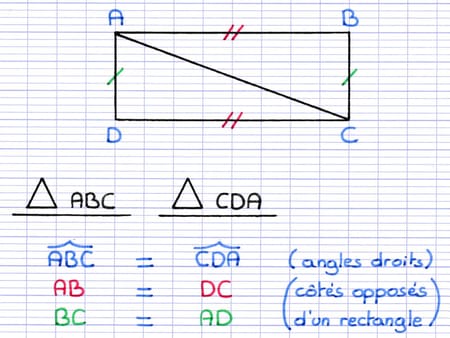
Démonstration que 2 triangles sont égaux avec le cas d’égalité CAC — [AB] et [DC] sont 2 côtés opposés d’un rectangle, ils ont donc la même longueur.

[BC] et [AD] sont 2 côtés opposés d’un rectangle, ils ont donc la même longueur.

Il s’agit de 2 paires de côtés de même longueur.

Les triangles ABC et CDA ont 1 paire d’angles de même mesure entre 2 paires de côtés de même longueur. On peut donc conclure que, d’après le cas d’égalité CAC, ces deux triangles sont égaux.

1 Côté entre 2 Angles (ACA)

On peut démontrer que deux triangles sont égaux en indiquant qu’ils ont 1 paire de côtés de même longueur entre 2 paires d’angles de même mesure. La démonstration commence en cherchant 1 paire de côtés de même longueur. Cette 1^ère paire de côtés apparait facilement puisque les deux triangles ont un côté commun.

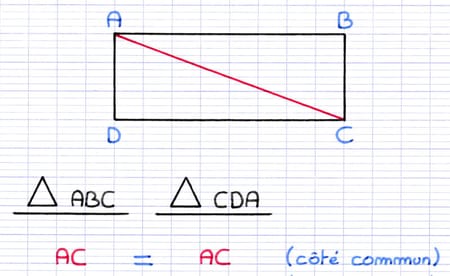
2 triangles ayant un côté commun — Le côté [AC] est commun aux 2 triangles. Il s’agit de la 1^ère paire de côtés de même longueur.

Pour compléter la démonstration, on doit indiquer que cette paire de côtés est entre 2 paires d’angles de même mesure. Ces 2 paires d’angles sont des paires d’angles alternes-internes. Puisque les droites (AB) et (DC) sont parallèles (côtés opposés d’un rectangle), ces angles alternes-internes ont la même mesure.

Fiche de Synthèse

Associer Droites Parallèles et Angles alternes-internes

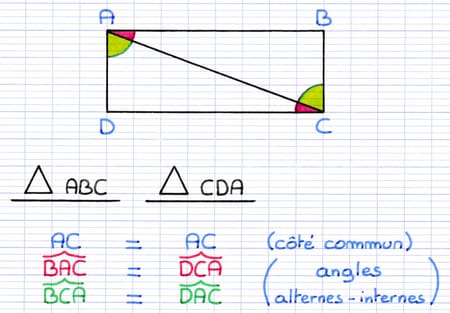
Démonstration que 2 triangles sont égaux avec le cas d’égalité ACA — BAC et DCA sont 2 angles alternes-internes de même mesure.

BCA et DAC sont 2 angles alternes-internes de même mesure.

Il s’agit de 2 paires d’angles de même mesure.

Les triangles ABC et CDA ont 1 paire de côtés de même longueur entre 2 paires d'angles de même mesure. On peut donc conclure que, d'après le cas d'égalité ACA, ces deux triangles sont égaux.