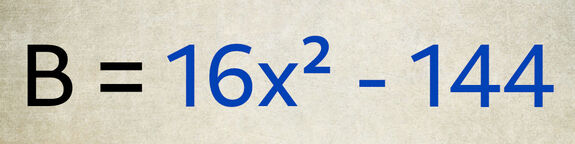Factoriser la Différence de Deux Carrés a²-b²
Théorie
L’expression littérale « a² - b² » est une différence de deux carrés. Sa factorisation s’effectue en appliquant la formule de l’identité remarquable.
Formule : « a² - b² = (a + b)(a - b) ».
Exemple
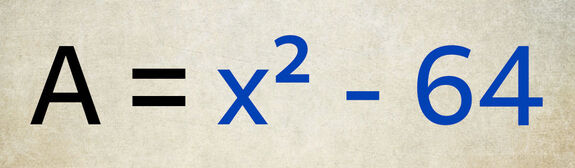
Comment factoriser « x² - 64 » ?
1. Obtenir la Différence de Deux Carrés
La première étape est de transformer l’expression littérale pour faire apparaître clairement une différence de deux carrés.
Si l’un des termes n’est pas écrit sous la forme d’un carré (une puissance dont l’exposant est « 2 »), on calcule sa racine carrée. En élevant le résultat obtenu au carré, on obtient un terme équivalent exprimé sous la forme d’un carré.
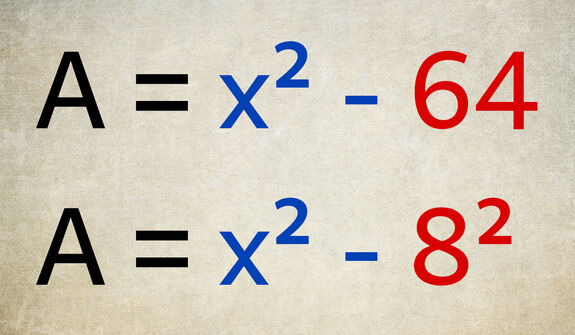
« 64 » n’est pas écrit sous la forme d’un carré.
« √64 = 8 » donc « 8² = 64 ».
« 64 » est remplacé par « 8² » pour obtenir la différence de deux carrés.
2. Identifier « a » et « b »
Pour factoriser l’identité remarquable « a² - b² », on identifie ensuite les valeurs de « a » et « b » :
- « a » est le premier terme élevé au carré.
- « b » est le deuxième terme élevé au carré.
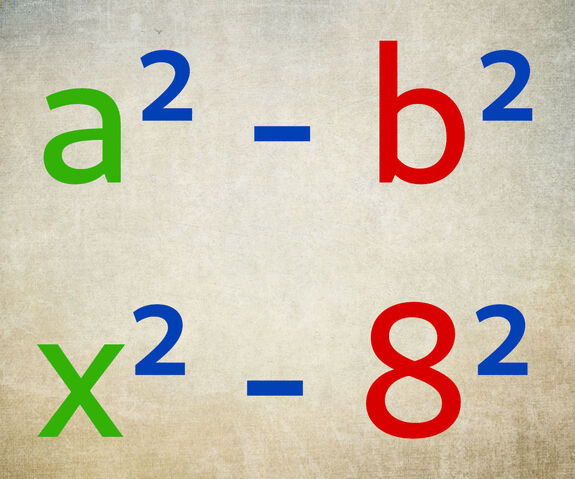
Au sein de l’identité remarquable :
La valeur de « a » est « x ».
La valeur de « b » est « 8 ».
3. Appliquer l’Identité Remarquable
Formule : « a² - b² = (a + b)(a - b) ».
D’après la formule de l’identité remarquable, la différence de deux carrés est égale au produit de la somme et de la différence des deux termes « a » et « b ».
Le résultat de la factorisation s’écrit donc sous la forme de deux parenthèses :
- La première parenthèse contient une somme : « (a + b) ».
- La deuxième parenthèse contient une différence : « (a - b) ».
Les deux parenthèses sont collées l’une à l’autre afin d’obtenir un produit (une multiplication). Ce produit est la forme factorisée de l’expression initiale.
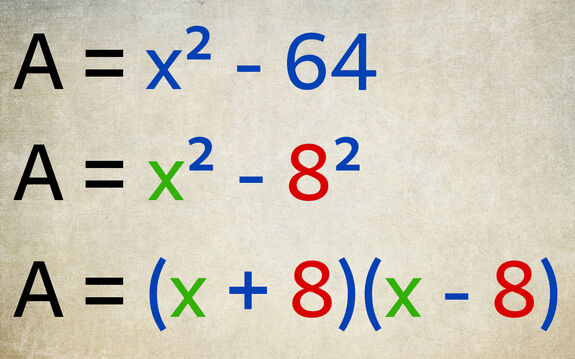
La forme factorisée de « x² - 64 » est « (x + 8)(x - 8) ».
Cas Particuliers
Terme sous Forme de Produit
L’expression à factoriser est parfois composée d’un terme écrit sous la forme d’un produit.
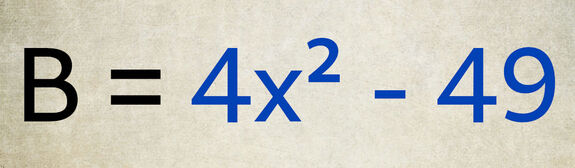
Le terme « 4x² » est le produit de « 4 » et de « x² ».
Puisque ce produit n’est pas sous la forme d’un carré (« x » est au carré, mais pas « 4 »), il faut transformer son écriture. Pour cela, on calcule la racine carrée du produit, et on note le résultat obtenu dans des parenthèses élevées au carré.
On obtient alors un terme équivalent exprimé sous la forme d’un carré. L’expression est ainsi correctement transformée en une différence de deux carrés.
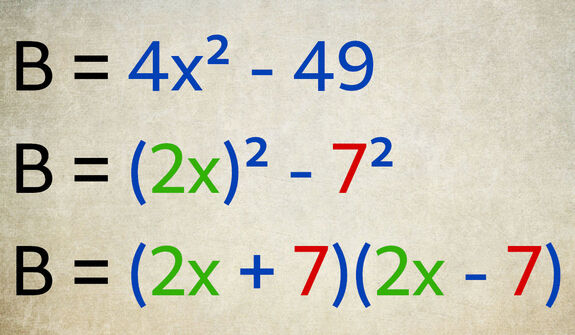
« √(4x²) = 2x » donc « (2x)² = 4x² ».
« 4x² » est remplacé par « (2x)² » afin d’obtenir la différence de deux carrés.
Absence de Carré Parfait
Dans les exemples précédents, chaque nombre au sein des expressions à factoriser était un carré parfait (4, 49, 64...). Ce n’est cependant pas toujours le cas.
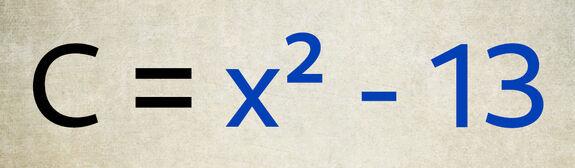
Il n’existe pas de nombre entier dont le carré est égal à « 13 ».
« 13 » n’est donc pas un carré parfait.
Il n’est pas possible de calculer précisément la racine carrée d’un nombre qui n’est pas un carré parfait. Pour obtenir une différence de deux carrés, on place ce nombre dans une racine carrée élevée au carré, sans calculer la racine.
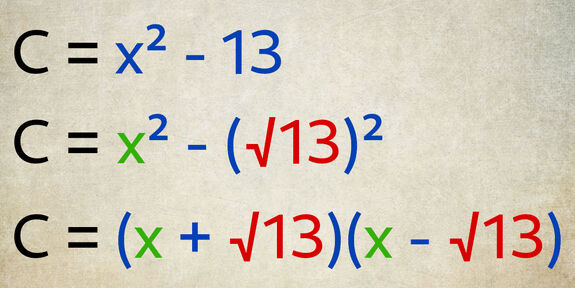
« (√13)² » est équivalent à « 13 », car racine et puissance se simplifient mutuellement.
Au sein de l’identité remarquable, la valeur de « b » est donc « √13 ».