Reconnaître et Décrire un Rectangle
Théorie
Un rectangle est un quadrilatère particulier qui possède 4 angles droits. Tous les rectangles partagent des caractéristiques communes.

ABCD est un rectangle.
4 Angles Droits
Le rectangle est un quadrilatère, il possède donc 4 angles dont la somme est égale à 360°. Ses angles ont la particularité d’être tous des angles droits (90°).
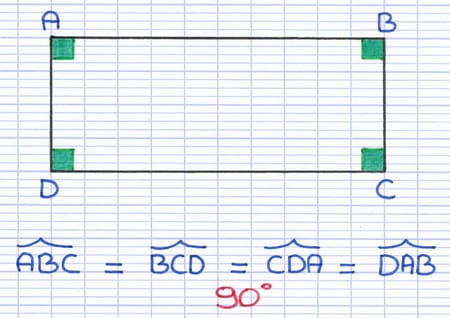
Ce rectangle possède 4 angles droits : ABC, BCD, CDA, DAB.
4 Côtés
Le rectangle est un quadrilatère, il possède donc 4 côtés. Ses côtés opposés (qui ne partagent pas un sommet commun) ont la particularité d’être parallèles et de la même longueur.
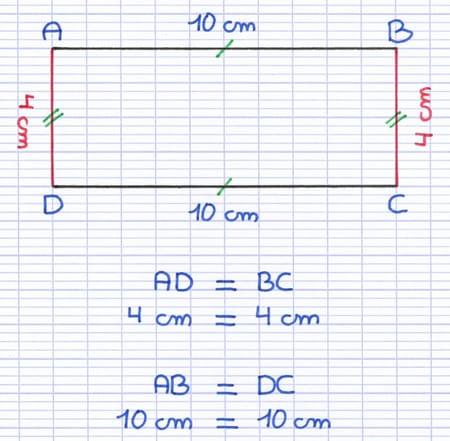
[AD] et [BC] sont 2 côtés opposés, ils sont parallèles et de même longueur.
[AB] et [DC] sont 2 côtés opposés, ils sont parallèles et de même longueur.
Les côtés consécutifs (qui partagent un sommet commun) du rectangle sont perpendiculaires. Ces côtés perpendiculaires forment un angle droit (90°).
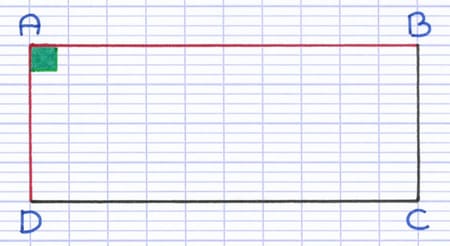
[AB] et [AD] sont 2 côtés consécutifs, ils sont perpendiculaires.
Le rectangle possède 2 longueurs et 2 largeurs :
- La longueur (L) du rectangle correspond à la mesure du plus grand côté.
- La largeur (l) du rectangle correspond à la mesure du plus petit côté.
Lorsque la longueur et la largeur d’un quadrilatère sont identiques, il s’agit d’un losange ou d’un carré.
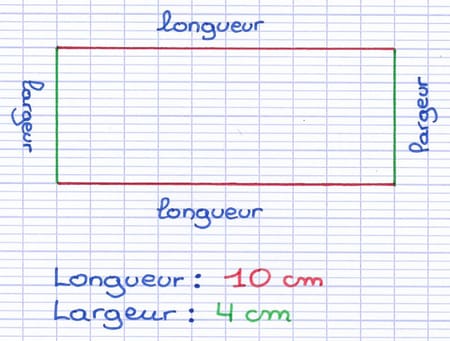
La longueur est le plus grand côté du rectangle.
La largeur est le plus petit côté du rectangle.
2 Diagonales
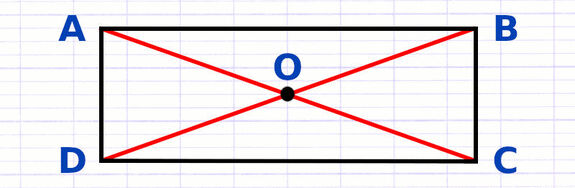
Le rectangle est un quadrilatère, il possède donc 2 diagonales qui relient les sommets opposés. Les diagonales du rectangle ont la particularité d’être de la même longueur et de se couper en leur milieu.
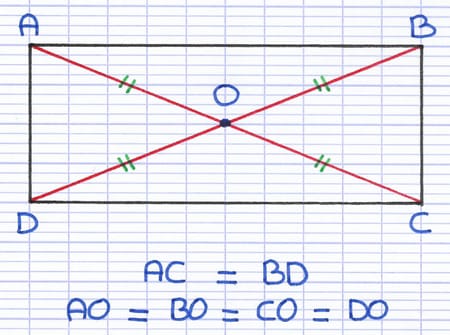
Le point O est le point d’intersection des 2 diagonales [AC] et [BD] du rectangle. La longueur AC est égale à la longueur BD. Les longueurs AO, BO, CO et DO sont identiques.
2 Axes de Symétrie
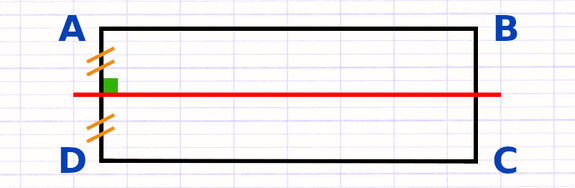
Un axe de symétrie est une droite qui coupe une figure géométrique en 2 parties superposables. Le rectangle possède 2 axes de symétrie : la médiatrice des longueurs et la médiatrice des largeurs. Une médiatrice est une droite qui coupe perpendiculairement un segment en son milieu.
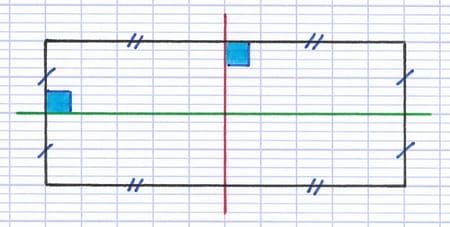
En rouge, l’axe de symétrie issue des longueurs.
En vert, l’axe de symétrie issue des largeurs.