Reconnaître les Parallélogrammes Particuliers
Théorie
Tous les parallélogrammes possèdent des caractéristiques communes :
- Les côtés opposés sont parallèles et de même longueur.
- Les angles opposés sont de même mesure.
- Les diagonales se coupent en leur milieu.
Certains parallélogrammes particuliers possèdent des caractéristiques supplémentaires.
Parallélogrammes particuliers
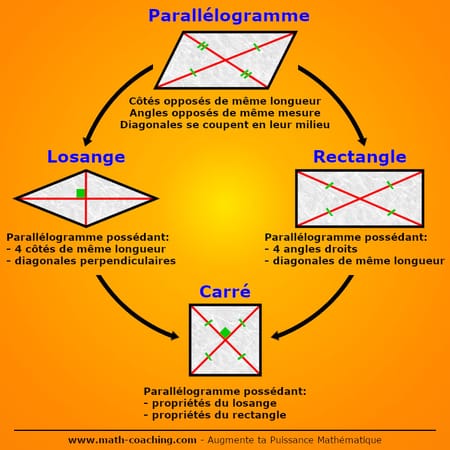
Le losange, le rectangle et le carré sont des parallélogrammes particuliers. Ils possèdent les propriétés des parallélogrammes, ainsi que quelques propriétés supplémentaires.
Losange
Le losange est un parallélogramme qui possède 2 caractéristiques supplémentaires :
- Les 4 côtés sont de même longueur.
- Les diagonales sont perpendiculaires.
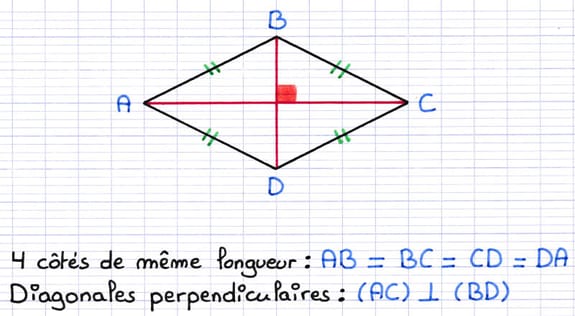
Le losange est un parallélogramme particulier.
Pour démontrer qu’un parallélogramme est un losange, on peut utiliser l’une des propriétés ci-dessous.
Propriété : "Si les côtés d’un parallélogramme sont de même longueur, alors c’est un losange".
Propriété : "Si les diagonales d’un parallélogramme sont perpendiculaires, alors c’est un losange".
Rectangle
Le rectangle est un parallélogramme qui possède 2 caractéristiques supplémentaires :
- Les 4 angles mesurent 90° (angle droit).
- Les diagonales sont de même longueur.
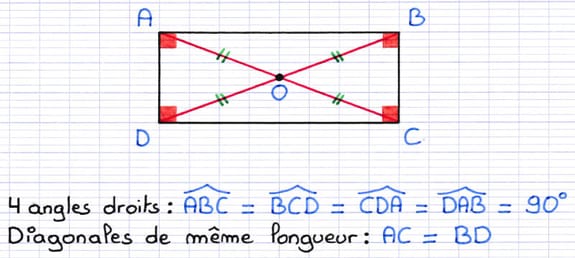
Le rectangle est un parallélogramme particulier.
Pour démontrer qu’un parallélogramme est un rectangle, on peut utiliser l’une des propriétés ci-dessous.
Propriété : "Si les angles d’un parallélogramme mesurent 90°, alors c’est un rectangle".
Propriété : "Si les diagonales d’un parallélogramme sont de même longueur, alors c’est un rectangle".
Carré
Le carré est un parallélogramme qui possède les caractéristiques du losange et du rectangle :
- Comme le losange, les 4 côtés sont de même longueur et les diagonales sont perpendiculaires.
- Comme le rectangle, les 4 angles mesurent 90° et les diagonales sont de même longueur.
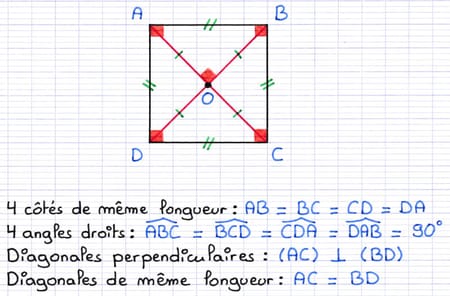
Le carré est un parallélogramme particulier.
Pour démontrer qu’un parallélogramme est un carré, on peut utiliser l’une des propriétés ci-dessous.
Propriété : "Si un parallélogramme possède 4 côtés de même longueur et 4 angles droits, alors c’est un carré".
Propriété : "Si un parallélogramme possède des diagonales perpendiculaires et de même longueur, alors c’est un carré".
Classification
Le parallélogramme est un quadrilatère particulier. Le losange, le rectangle et le carré sont des parallélogrammes particuliers. Le carré est à la fois un losange particulier et un rectangle particulier.
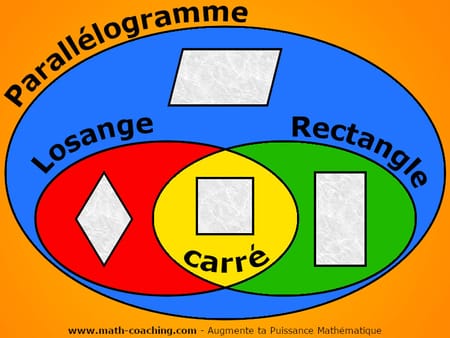
Classification des parallélogrammes particuliers au sein d’un diagramme de Venn.
