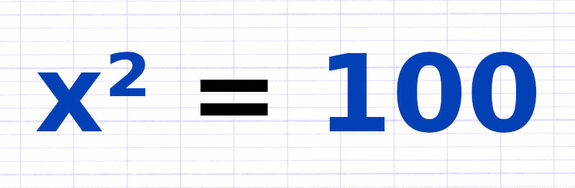Résoudre une Équation dont l’Inconnue est au Carré

🎯

Questions validées : 0 / 3

Théorie

Résoudre une équation consiste à trouver la valeur de l’inconnue (généralement "x"). Lorsque l’équation est de la forme "x² = a" ("a" étant un nombre donné), on cherche les nombres dont le carré est égal à "a".

Ce type d’équation admet généralement 2 solutions (une positive et une négative). Ces solutions sont obtenues en ayant recours aux racines carrées.

★

Exemple

★

Équation à résoudre avec une inconnue au carré : x² = 37. — Comment résoudre cette équation dont l’**inconnue** est **au carré** ?

Trouver la Solution Positive

Propriété : "Le carré de la racine carrée d’un nombre positif est égal à ce nombre."

Cette propriété est importante à connaître pour résoudre une équation dont l’inconnue est au carré. Elle signifie que le carré et la racine carrée se simplifient mutuellement. Cette simplification est possible, car le carré est l’inverse de la racine carrée.

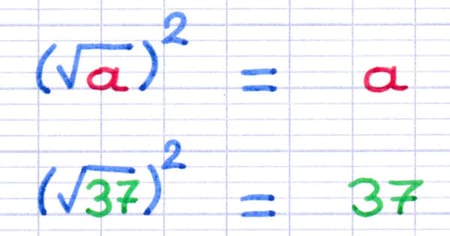
Calcul du carré de la racine carrée : (√a)² = a donc (√37)² = 37. — Le carré de la racine carrée de 37 est égal à 37.

Fiche de Synthèse

Simplifier une Puissance avec une Racine Carrée

Cette propriété permet de trouver la solution positive de l’équation. Cette 1^re solution est obtenue en répondant à la question suivante : "Quel est le nombre positif dont le carré est égal à 37 ?". Pour y répondre, il suffit d’utiliser la propriété précédente (le carré de la racine carrée de 37 est égal à 37).

La solution positive de l’équation est la racine carrée de 37. — La **solution positive** de l’équation est la racine carrée de 37 (√37).

Trouver la Solution Négative

Propriété : "Le carré d’un nombre négatif est égal à un nombre positif."

Cette propriété est importante à connaître pour trouver la solution négative de l’équation. Elle repose sur la règle des signes, selon laquelle le produit de 2 nombres négatifs est toujours un nombre positif.

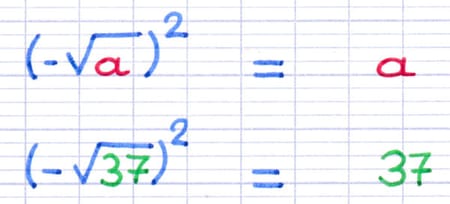
Calcul du carré d’un nombre négatif : (−√a)² = a donc (−√37)² = 37. — Le carré de la racine carrée négative de 37 est égal à 37.

Grâce à cette propriété, on peut répondre facilement à la question suivante : "Quel est le nombre négatif dont le carré est égal à 37 ?". La réponse à cette question est la solution négative de l’équation. Elle est obtenue en plaçant tout simplement un signe moins ("-") devant la solution précédente.

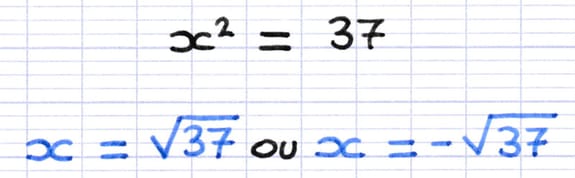
La solution négative de l’équation est −√37. — La **solution négative** de l’équation est la racine carrée négative de 37 (-√37).

Noter les Solutions de l’Équation

En règle générale, une équation dont l’inconnue est au carré admet 2 solutions (une positive et une négative). Ces 2 solutions se notent dans des accolades : "S = {solution 1 ; solution 2}". Dans les accolades, les solutions sont classées par ordre croissant et séparées par un point-virgule.

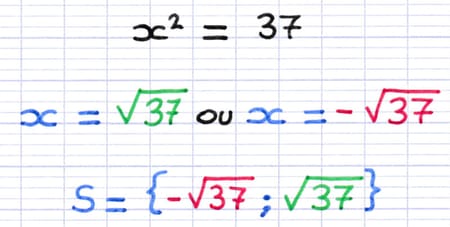
Les deux solutions de l’équation dont l’inconnue est au carré notée dans des accolades : S = {−√37 ; √37}. — Les **2 solutions** de l’équation sont placées dans des accolades.

★

Cas particuliers

★

Lorsque l’inconnue au carré est égale à 0, l’équation admet 1 unique solution. Cette unique solution est le chiffre 0.

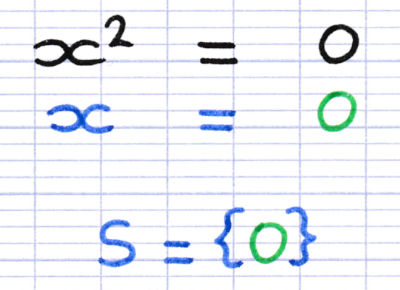
Cas particulier d’équation où l’inconnue au carré est égale à zéro : x² = 0 donc avec x = 0, S = {0}. — Quel nombre au carré est égal à 0 ? C’est 0 !

Lorsque l’inconnue au carré est égale à un nombre négatif, l’équation n’admet aucune solution. Il n’existe aucun nombre dont le carré est égal à un nombre négatif.

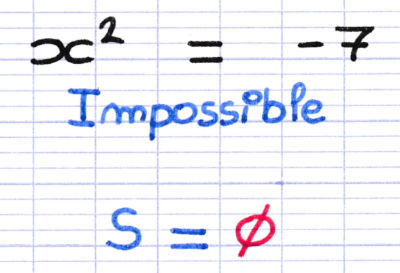
Cas particulier d’équation où l’inconnue au carré est égale à un nombre négatif : x² = −7 impossible à résoudre, S = ∅. — Quel nombre au carré est égal à un nombre négatif ? Aucun ! L’absence de solution est symbolisée par un rond barré : ∅.

Lorsque l’inconnue au carré est égale à un carré parfait, les 2 solutions sont des nombres entiers. En effet, la racine carrée d’un carré parfait est égale à un nombre entier.