Additionner les Probabilités des Issues d’une Expérience
Théorie
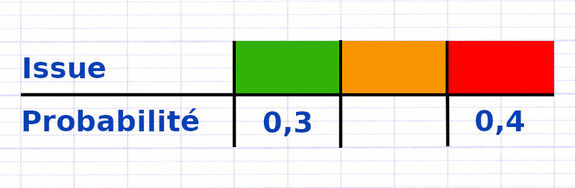
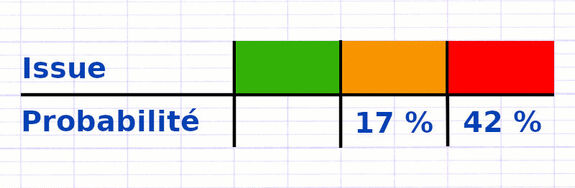
Propriété : "La somme des probabilités de toutes les issues d’une expérience aléatoire est égale à 1".
En probabilité, une issue est un résultat possible d’une expérience aléatoire. Lorsqu’on additionne les probabilités de toutes les issues, on obtient toujours un total de 1.
Exemple
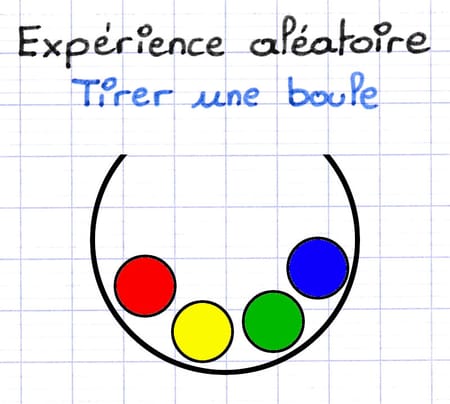
Comment additionner les probabilités des issues de cette expérience aléatoire ?
Identifier les Issues
La probabilité de chaque issue dépend du nombre total d’issues de l’expérience. La 1re étape est donc d’identifier toutes les issues possibles. L’ensemble des issues forme l’univers (Ω) de l’expérience aléatoire.
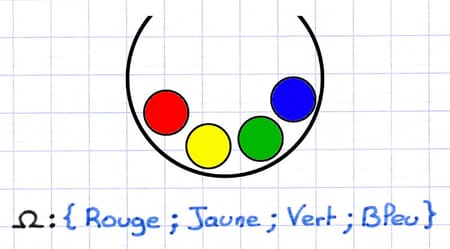
Cette expérience aléatoire possède 4 issues :
1) Obtenir une boule rouge.
2) Obtenir une boule jaune.
3) Obtenir une boule verte.
4) Obtenir une boule bleue.
Calculer Chaque Probabilité
La 2e étape est de déterminer la probabilité que chaque issue se réalise. En situation d’équiprobabilité, la probabilité de chaque issue est une fraction identique :
- Le numérateur est le chiffre 1.
- Le dénominateur est le nombre total d’issues (4).
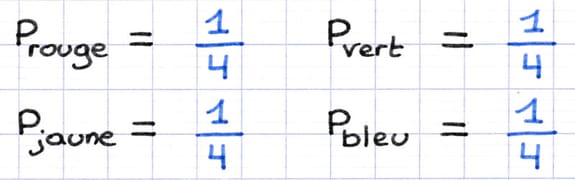
La probabilité de chaque issue est de 1/4.
Additionner les Probabilités
La dernière étape est d’additionner les probabilités de chaque issue. La somme des probabilités de toutes les issues est toujours égale à :
- 1 si les probabilités sont exprimées en fractions ou nombres décimaux.
- 100 % si les probabilités sont exprimées en pourcentages.
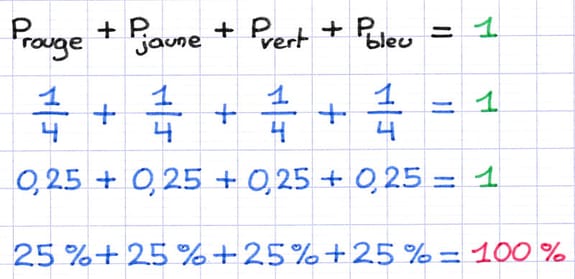
L’addition des probabilités de toutes les issues est égale à 1.
Exercices
Question 1
On tire au hasard une boule dans une urne contenant des boules vertes, oranges et rouges. Quelle est la probabilité de tirer une boule orange ?
Question 2
Laquelle de ces propositions est fausse ?
Question 3
On tire au hasard une boule dans une urne contenant des boules vertes, oranges et rouges. Quelle est la probabilité de tirer une boule verte ?