Calculer la Longueur d’un Côté d’un Triangle Rectangle

🎯

Questions validées : 0 / 3

Théorie

Théorème de Pythagore : "Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés".

Le théorème de Pythagore permet de calculer la longueur d’un côté d’un triangle rectangle, à condition de connaitre la longueur des deux autres côtés.

★

Exemple

★

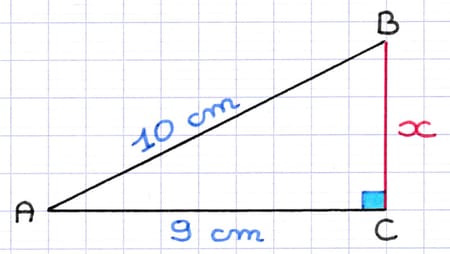
Triangle ABC rectangle en C dont on cherche à calculer la longueur BC. — Comment calculer la longueur du côté [BC] de ce triangle rectangle ?

Mettre en Équation le Théorème de Pythagore

La 1^re étape est de mettre en équation le théorème de Pythagore. Pour cela, on a besoin de la longueur de chaque côté du triangle rectangle :

Longueur de l’hypoténuse : 10 cm.
Longueur des 2 autres côtés : x (valeur inconnue) et 9 cm.

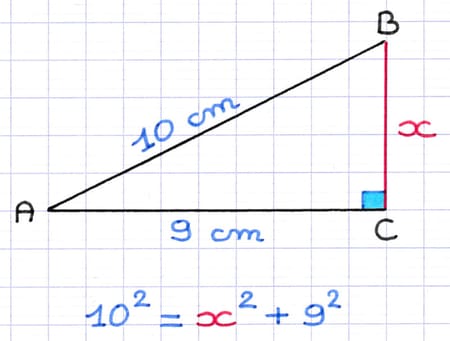
Le théorème de Pythagore est mis en équation : 10² = x² + 9². — **Pythagore :** Le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.

**Équation :** 10² = x² + 9².

Isoler l’Inconnue

Pour trouver la longueur du 3^e côté, il faut résoudre l’équation de Pythagore. La résolution de l’équation s’effectue en isolant l’inconnue (x²) au sein de l’équation. Pour y parvenir, on regroupe les termes indépendants du même côté de l’équation. Cette étape s’effectue en changeant le signe du terme qui se déplace de l’autre côté du signe égal.

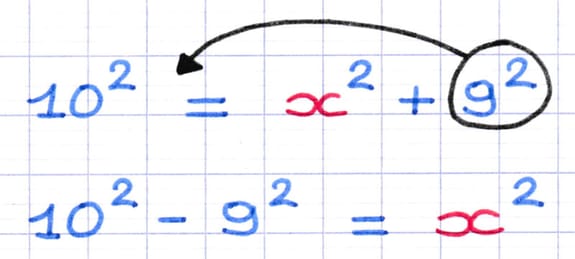
Au sein de l’équation de Pythagore, l’inconnue est déplacée afin d’être isolée. — +9² se déplace de l’autre côté du signe égal et devient -9². L’inconnue x² est ainsi isolée à droite du signe égal.

Fiche de Synthèse

Résoudre une Équation du Premier Degré

Effectuer les Calculs

L’étape suivante est de réduire l’équation en effectuant les calculs. En appliquant l’ordre de priorité des opérations (PEMDAS), on calcule d’abord le carré de chaque longueur, puis on soustrait les deux résultats obtenus.

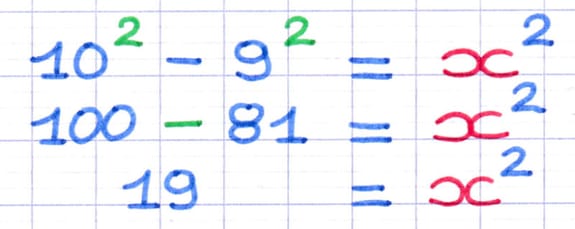
Les calculs sont effectués au sein de l’équation de Pythagore : 10² − 9² = x², 100 − 81 = x², 19 = x². — On calcule d’abord les puissances, puis on soustrait les résultats.

Fiche de Synthèse

Calculer la Puissance d’un Nombre

Trouver la Solution de l’Équation

La dernière étape est de transformer l’inconnue x² en x afin d’obtenir la solution de l’équation. Cette transformation s’effectue en faisant apparaître une racine carrée. La valeur de l’inconnue correspond à la longueur du 3^e côté du triangle rectangle.

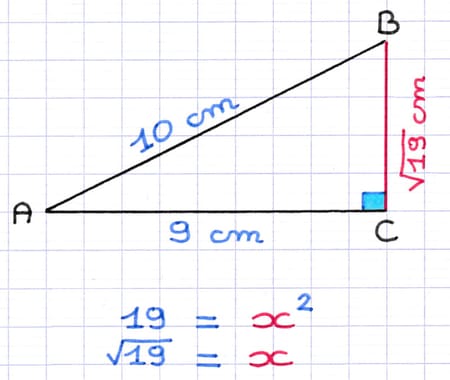
La longueur du côté BC du triangle rectangle est la solution de l’équation de Pythagore : √19 cm. — La **solution de l’équation** de Pythagore est √19. La longueur du côté BC du triangle rectangle est donc de √19 cm.

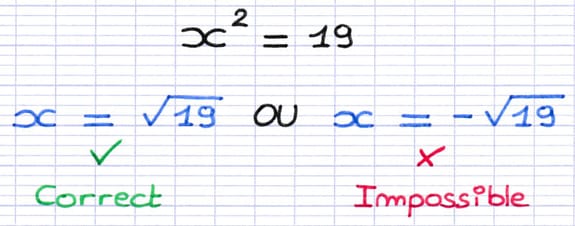
En règle générale, une équation dont l’inconnue est au carré (x²) possède deux solutions (une positive et une négative). Toutefois, l’inconnue dans une équation de Pythagore est une longueur, elle ne peut donc pas être négative. La longueur d’un côté d’un triangle rectangle est toujours positive.