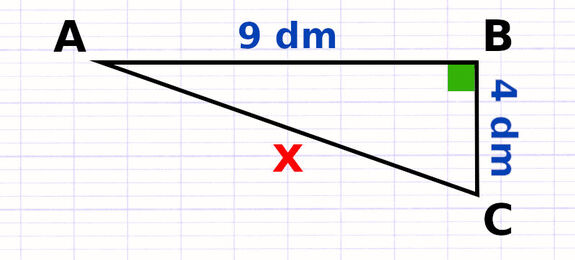
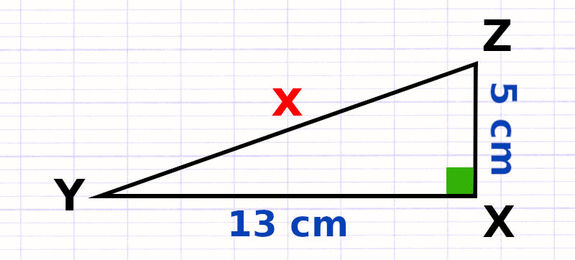
Calculer la Longueur d’une Hypoténuse avec Pythagore

🎯

Questions validées : 0 / 3

Théorie

Théorème de Pythagore : "Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés".

Grâce au théorème de Pythagore, on peut calculer la longueur d’une hypoténuse si on connaît la longueur des deux autres côtés du triangle rectangle.

★

Exemple

★

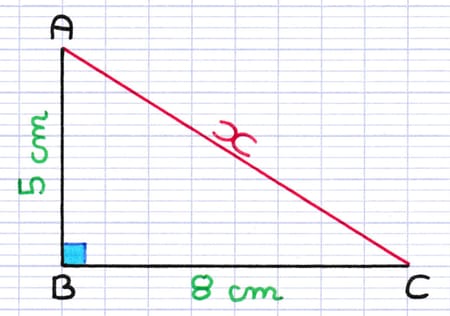
Calculer la longueur d’une hypotenuse avec le théorème de Pythagore — Comment calculer la longueur de cette hypoténuse avec le **théorème de Pythagore** ?

1. Mettre le Théorème en Équation

La 1^ère étape est de mettre en équation le théorème de Pythagore. Pour cela, on observe le triangle rectangle à la recherche de :

La longueur de l’hypoténuse : x (valeur inconnue).
La longueur des 2 autres côtés : 8 cm et 5 cm.

Grâce à ces informations, on peut écrire le théorème de Pythagore sous la forme d’une équation.

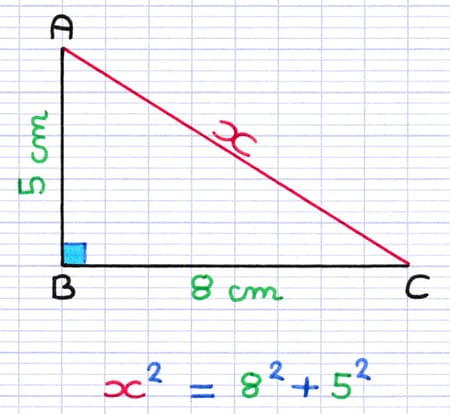
Transformation du théorème de Pythagore en équation mathématique — **Théorème :** Le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.

**Équation :** x² = 8² + 5².

2. Calculer la Somme des Carrés

L’étape suivante est de calculer, au sein de l’équation, la somme des carrés des longueurs des deux autres côtés. Il est important de respecter l’ordre de priorité des opérations (PEMDAS) selon lequel les carrés sont effectués avant les additions.

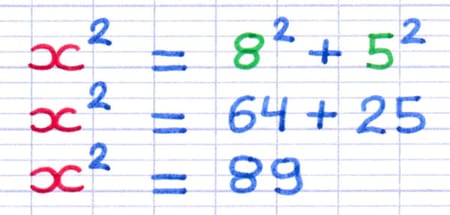
Calcul de la somme des carrés des longueurs des 2 autres côtés — La somme des carrés des longueurs des deux autres côtés est 89.

3. Trouver la Longueur Exacte de l'Hypoténuse

Pour trouver la longueur exacte de l’hypoténuse, il suffit maintenant de résoudre l’équation. Puisque l’inconnue est au carré (x²), la résolution s’effectue à l’aide d’une racine carrée. La solution de l’équation est la longueur exacte de l’hypoténuse du triangle rectangle.

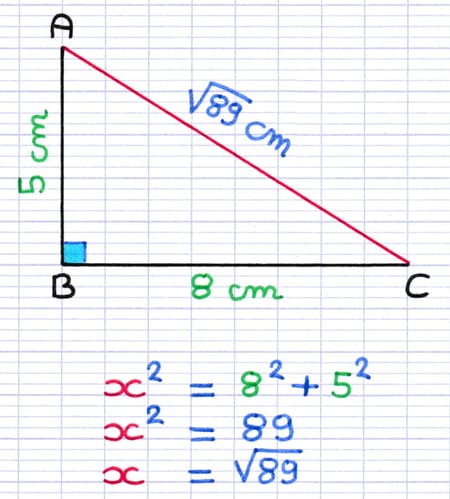
Longueur exacte de l’hypoténuse d’un triangle rectangle — La longueur exacte de l’**hypoténuse** est de √89 cm.

Une équation dont l’inconnue est au carré admet en général 2 solutions (une positive et une négative). Cependant, lorsque l’inconnue représente une longueur, seule la solution positive est admise. La longueur d’une hypoténuse est toujours positive, jamais négative.

La solution positive de l’équation est la longueur de l’hypoténuse — La longueur de l’hypoténuse est la **solution positive** de l’équation.

Fiche de Synthèse

Résoudre une Équation dont l'Inconnue est au Carré

4. Trouver la Valeur Approchée de l'Hypoténuse

Lorsque la longueur de l’hypoténuse est une racine carrée, on peut en extraire une valeur approchée. La valeur approchée est un nombre décimal arrondi à partir d’un certain rang :