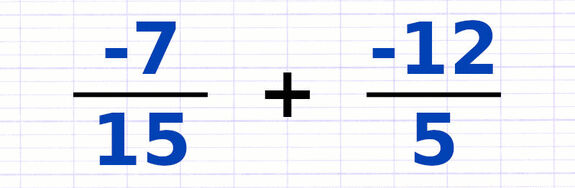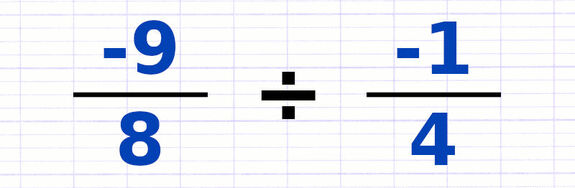Appliquer la Règle des Signes aux Fractions
Théorie
La règle des signes s’applique dans 2 situations :
- Lorsque des signes positifs ou négatifs (+/-) sont l’un à côté de l’autre.
- Lorsqu’on multiplie ou divise des nombres relatifs (nombres positifs / négatifs).
Il est donc important de respecter la règle des signes lorsqu’on additionne, soustrait, multiplie ou divise des fractions composées de nombres relatifs.
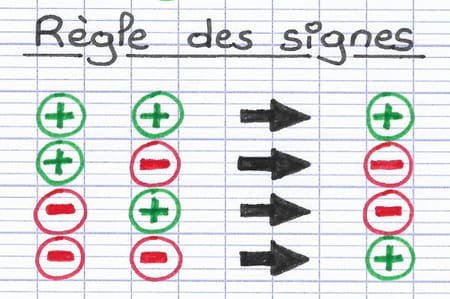
2 signes positifs fusionnent en 1 signe positif.
1 signe positif et négatif fusionnent en 1 signe négatif.
1 signe négatif et positif fusionnent en 1 signe négatif.
2 signes négatifs fusionnent en 1 signe positif.
Exemples
Addition de Fractions
Comment additionner ces fractions composées de nombres relatifs ?
La 1ère étape est de placer les 2 fractions sur un dénominateur commun afin de pouvoir les additionner. Le dénominateur commun est le plus petit commun multiple des dénominateurs.
Les 2 fractions à additionner sont placées sur un dénominateur commun.
Lorsque le numérateur d’une fraction est négatif, on peut placer le signe "-" devant la fraction. De cette façon, on fait apparaître 2 signes l’un à côté de l’autre. Ces signes peuvent ensuite fusionner en appliquant la règle des signes.
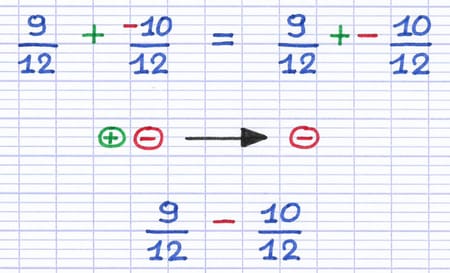
D’après la règle des signes, 1 signe positif et négatif fusionnent en 1 signe négatif. L’addition de fractions est transformée en soustraction.
En appliquant la règle des signes, on se retrouve désormais face à une soustraction de fractions. La dernière étape est d’effectuer la soustraction.
Pour soustraire 2 fractions, on soustrait simplement leurs numérateurs.
9 - 10 = -1.
Soustraction de Fractions
Comment soustraire ces fractions composées de nombres relatifs ?
Lorsqu’un dénominateur est négatif, on peut déplacer le signe "-" au numérateur ou devant la fraction. La 1ère étape consiste à déplacer le signe négatif de la 2ème fraction devant la fraction. De cette façon, on fait apparaître 2 signes l’un à côté de l’autre. Ces signes peuvent ensuite fusionner en appliquant la règle des signes.
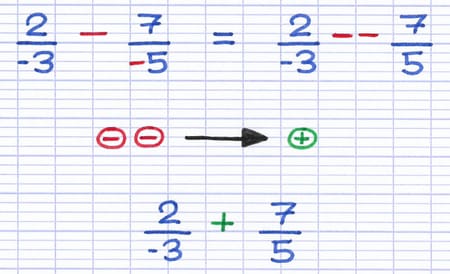
D’après la règle des signes, 2 signes négatifs fusionnent en 1 signe positif. La soustraction de fractions est transformée en addition.
En appliquant la règle des signes, on se retrouve désormais face à une addition de fractions. L’étape suivante est de placer les 2 fractions sur un dénominateur commun. Il est cependant impossible de trouver un dénominateur commun si les dénominateurs ont des signes différents. Il faut donc au préalable déplacer le signe négatif du dénominateur au numérateur afin d’obtenir 2 dénominateurs positifs.
Les dénominateurs doivent être de signe identique pour trouver un dénominateur commun.
L’étape finale est d’additionner les deux fractions.
Pour additionner 2 fractions, on additionne simplement leurs numérateurs.
-10 + 21 = 11.
Multiplication de Fractions
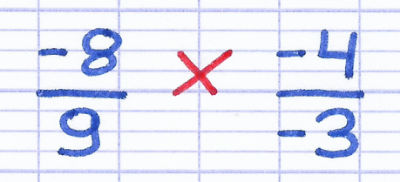
Comment multiplier ces fractions composées de nombres relatifs ?
Lorsque le numérateur et le dénominateur d’une fraction sont négatifs, on applique directement la règle des signes. Les 2 signes négatifs de la fraction fusionnent pour former 1 signe positif.
D’après la règle des signes, 2 signes négatifs fusionnent en 1 signe positif. Il n’est pas nécessaire de noter le signe positif.
On peut ensuite procéder à la multiplication des deux fractions en respectant la règle des signes.
Pour multiplier 2 fractions, on multiplie les numérateurs et les dénominateurs séparément.
-8 x 4 = -32.
9 x 3 = 27.
Division de Fractions
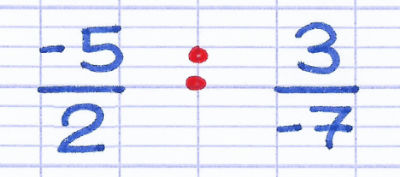
Comment diviser ces fractions composées de nombres relatifs ?
La 1ère étape est de transformer la division en multiplication. En contrepartie, la 2ème fraction est inversée (le numérateur devient le dénominateur, et vice versa).
Transformation de la division de fractions en multiplication. L’inverse de 3/-7 est -7/3.
On peut ensuite multiplier les deux fractions en appliquant la règle des signes.
D’après la règle des signes, 2 signes négatifs fusionnent en 1 signe positif.
-5 x -7 = 35.
2 x 3 = 6.
Exercice
Question 1
Quel est le résultat de l’addition de ces deux fractions ?
Question 2
Quel est le résultat de la division de ces deux fractions ?
Question 3
Quel est le résultat de la soustraction de ces deux fractions ?